题目内容
8.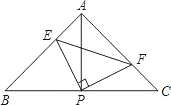 已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下结论:
已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下结论:①EF=AP;
②△APF和△CPF可以分别看作由△BPE和△APE绕点P顺时针方向旋转90°得到的;
③△EPF是等腰直角三角形;
④S△ABC=2S四边形AEPF.
其中始终成立的有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 先利用△ABC为等腰直角三角形得到∠B=∠C=45°,再利用等腰三角形的性质得到AP⊥BC,AP平分∠BAC,AP=BP=CP,于是可证明△BPE≌△APF,所以BE=AF,PE=PF,于是可判定△PEF为等腰直角三角形,EF=$\sqrt{2}$PE,由于当PE⊥AB时,AP=$\sqrt{2}$PE,所以EF与AP不一定相等;利用旋转的定义可对②进行判断;最后利用△BPE≌△APF得到S△BPE=S△APF,所以S四边形AEPF=S△ABC,从而得到S△ABC=2S四边形AEPF.
解答 解:∵AB=AC,∠BAC=90°,
∴△ABC为等腰直角三角形,
∴∠B=∠C=45°,
∵P点为BC的中点,
∴AP⊥BC,AP平分∠BAC,AP=BP=CP,
∵∠EPF=90°,
∴∠BPE=∠APF,
在△BPE和△APF中
$\left\{\begin{array}{l}{∠B=∠APF}\\{PB=PA}\\{∠BPE=∠APF}\end{array}\right.$,
∴△BPE≌△APF,
∴BE=AF,PE=PF,
∴△PEF为等腰直角三角形,所以③正确;
∴EF=$\sqrt{2}$PE,
而当PE⊥AB时,AP=$\sqrt{2}$PE,
所以①错误;
∵PB=PA,PE=PF,∠BPA=∠APF=90°,
∴△PBE绕点P顺时针旋转90°可得到△PAF,
同理可得△PAE绕点P顺时针旋转90°可得到△PCF,
所以②正确;
∵△BPE≌△APF,
∴S△BPE=S△APF,
∴S四边形AEPF=S△AEP+S△APF=S△APE+S△PBE=S△ABC,
∴S△ABC=2S四边形AEPF.
所以④正确.
故选B
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等边三角形的性质和勾股定理的逆定理.也考查了等腰直角三角形的性质,会利用全等三角形的知识解决线段相等的问题.

| A. | 同圆或等圆中,等现所对的圆周角相等 | |
| B. | 圆的切线垂直于半径 | |
| C. | 三角形的内心是三角形角平分线的交点 | |
| D. | 平分弦的直径垂直于弦 |
 如图,直线y=3x和y=kx+2相交于点P(a,3),则关于x不等式(3-k)x≤2的解集为x≤1.
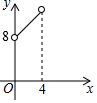
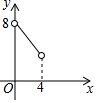
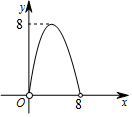
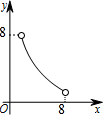
如图,直线y=3x和y=kx+2相交于点P(a,3),则关于x不等式(3-k)x≤2的解集为x≤1.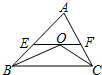 如图,在△ABC中,点O是△ABC的内心,连接OB,OC,过点O作EF∥BC分别交AB,AC于点E,F.已知△ABC的周长为8,BC=x,△AEF的周长为y,则表示y与x的函数图象大致是( )
如图,在△ABC中,点O是△ABC的内心,连接OB,OC,过点O作EF∥BC分别交AB,AC于点E,F.已知△ABC的周长为8,BC=x,△AEF的周长为y,则表示y与x的函数图象大致是( )