题目内容
18．若a+$\frac{1}{a}$=m，则$\frac{{a}^{4}+1}{{a}^{2}}$等于m-2．分析 先根据a+$\frac{1}{a}$=m，得a2+1=ma，再整体代入即可得出答案．
解答 解：∵a+$\frac{1}{a}$=m，
∴a2+1=ma，
∴$\frac{{a}^{4}+1}{{a}^{2}}$=$\frac{（ma-1）^{2}+1}{ma-1}$
=$\frac{m{a}^{2}-2ma+2}{ma-1}$
=$\frac{m（ma-1）-2ma+2}{ma-1}$
=$\frac{{m}^{2}a-m-2ma+2}{ma-1}$
=$\frac{m（ma-1）-2（ma-1）}{ma-1}$
=m-2．
故答案为m-2．
点评 本题考查了分式的混合运算，把分式化到最简，再整体代入是解答的关键．
练习册系列答案
相关题目
13．一个小球由静止开始在一个斜披上向下滚动，通过一次观察到小球的距离s（m）与时间t（s）的数据如下表所示：
写出用t表示s的函数关系式：s=2t+4．
| t/s | 1 | 2 | 3 | 4 | … |
| s/m | 6 | 8 | 10 | 12 | … |
甲驾车从A地去往B地，到达后停留3个小时，然后返回，往返车速都为120千米/时，乙驾车从B地去往A地，到达后停留1.5小时，因事提前返回，乙往返的车速不变，如图是两车距A地的路程s（千米0与行驶时间t（小时）之间的函数图象，请结合图象回答下列问题：
已知两条直线l1、l2分别经过点A（-1，0）、点B（3，0）并且当两条直线同时相交于y轴的负半轴上的点C时，恰好有l1⊥l2，经过点A、B、C的抛物线的对称轴与直线l1交于点K，与直线l2交于点E，在x轴交于点F，D是抛物线的顶点，如图所示．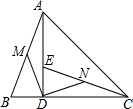
如图，在△ABC中，AD⊥BC，垂足为D，AD=CD，点E在AD上，DE=BD，M、N分别是AB、CE的中点．