已知两条直线l1.l2分别经过点A并且当两条直线同时相交于y轴的负半轴上的点C时.恰好有l1⊥l2.经过点A.B.C的抛物线的对称轴与直线l1交于点K.与直线l2交于点E.在x轴交于点F.D是抛物线的顶点.如图所示．(1)求点C的坐标.并求出抛物线的函数解析式,(2)抛物线的对称轴被直线l1.抛物线.直线l2和x轴依次截得三条线段.问:这三条线段有何数量关系?请说明理由� 题目和参考答案——青夏教育精英家教网—

题目内容

3．

已知两条直线l₁、l₂分别经过点A（-1，0）、点B（3，0）并且当两条直线同时相交于y轴的负半轴上的点C时，恰好有l₁⊥l₂，经过点A、B、C的抛物线的对称轴与直线l₁交于点K，与直线l₂交于点E，在x轴交于点F，D是抛物线的顶点，如图所示．
（1）求点C的坐标，并求出抛物线的函数解析式；
（2）抛物线的对称轴被直线l₁、抛物线、直线l₂和x轴依次截得三条线段，问：这三条线段有何数量关系？请说明理由．
（3）当直线l₂绕点C旋转时，与抛物线的另一个交点为M，请找出使△MCK为等腰三角形的点M，简述理由，并写出点M的坐标．

分析（1）利用△BOC∽△COA，根据相似三角形的性质求得OC的长，则C的坐标即可求得，然后利用待定系数法求得二次函数的解析式；
（2）首先求得l₁，l₂和抛物线的对称轴的解析式，进而求得K、D、E、F分坐标，则DK、DE、和EF的关系即可求得；
（3）分成K、C、M分别是等腰三角形的顶点三种情况进行讨论，根据等腰三角形的性质求解．

解答解：（1）由题意可得AO=1，BO=3，
∵△BOC∽△COA，
∴$\frac{CO}{BO}$=$\frac{AO}{CO}$，即$\frac{CO}{3}$=$\frac{1}{CO}$，
∴CO=$\sqrt{3}$或-$\sqrt{3}$（舍去）．
∴C的坐标是（0，-$\sqrt{3}$）．
设抛物线的解析式是y=ax²+bx+c，
根据题意得：$\left\{\begin{array}{l}{a-b-c=0}\\{9a+3b+c=0}\\{c=-\sqrt{3}}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{a=\frac{\sqrt{3}}{3}}\\{b=-\frac{2\sqrt{3}}{3}}\\{c=-\sqrt{3}}\end{array}\right.$，
则抛物线的解析式是y=$\frac{\sqrt{3}}{3}$x²-$\frac{2\sqrt{3}}{3}$x-$\sqrt{3}$；
（2）所得的三条线段的数量关系是KD=DE=EF．
理由是：设直线l₁的解析式是y=kx+b，
则$\left\{\begin{array}{l}{-k+b=0}\\{b=-\sqrt{3}}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{k=-\sqrt{3}}\\{b=-\sqrt{3}}\end{array}\right.$，
则直线l₁的解析式是y=-$\sqrt{3}$x-$\sqrt{3}$．
同理l₂的解析式是y=$\frac{\sqrt{3}}{3}$x-$\sqrt{3}$．
抛物线的对称轴是x=1，
则K的坐标是（1，-2$\sqrt{3}$），D的坐标是（1，-$\frac{4\sqrt{3}}{3}$），E的坐标是（1，-$\frac{2\sqrt{3}}{3}$），F的坐标是（1，0）．
则KD=$\frac{2\sqrt{3}}{3}$，DE=$\frac{2\sqrt{3}}{3}$，EF=$\frac{2\sqrt{3}}{3}$．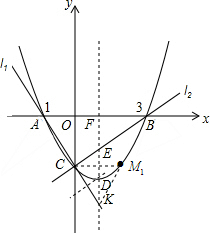
则KD=DE=EF；
（3）由题意需进行分类讨论．
①以K为圆心，KC的长为半径画圆弧，交抛物线于点M₁，此时KM₁=KC，则M₁与C关于对称轴x=1对称．
设M₁的横坐标是a，则$\frac{1}{2}$a=1，解得：a=2．
则M₁的坐标是（2，-$\sqrt{3}$）；
②当以点C为圆心，线段KC的长为半径画圆弧时，与抛物线的交点M₁和A，而A、C、K三点在一条直线上，不能构成三角形；
③作线段KC的中垂线，
∵CD=$\sqrt{{1}^{2}+（-\sqrt{3}+\frac{4\sqrt{3}}{3}）^{2}}$=$\frac{2\sqrt{3}}{3}$，
∴CD=DK．
∴KC的中垂线一定经过D．
即此时D就是所求的点M₂．此时有点M₂，即点M₂的坐标是（1，-$\frac{4\sqrt{3}}{3}$）使得△M₂CK是等腰三角形．
综上所述，当点M的坐标是（2，-$\sqrt{3}$），（1，-$\frac{4\sqrt{3}}{3}$）时，△MCK是等腰三角形．