题目内容
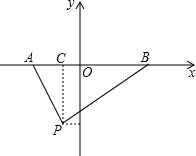 求如图,已知点A(-4,0)和点B(6,0),第三象限内有一点P,它的横坐标为-2,并且满足条件tan∠PAB•tan∠PBA=1.
求如图,已知点A(-4,0)和点B(6,0),第三象限内有一点P,它的横坐标为-2,并且满足条件tan∠PAB•tan∠PBA=1.(1)求证:△PAB是直角三角形;
(2)求过P、A、B三个点的抛物线的表达式,并求顶点坐标.
考点:二次函数综合题
专题:压轴题
分析:(1)过点P作PC⊥AB于C,根据锐角三角函数的正切值的定义列式整理可得
=
,然后求出△ACP和△PCB相似,根据相似三角形对应角相等可得∠PAC=∠BPC,再求出∠APB=90°,然后根据直角三角形的定义证明即可;
(2)根据点A、B的坐标和点P的横坐标求出AC、BC,再求出PC,然后写出点P的坐标,再利用待定系数法求二次函数解析式即可.
| PC |
| AC |
| BC |
| PC |
(2)根据点A、B的坐标和点P的横坐标求出AC、BC,再求出PC,然后写出点P的坐标,再利用待定系数法求二次函数解析式即可.
解答:(1)证明:如图,过点P作PC⊥AB于C,
∵tan∠PAB•tan∠PBA=1,
∴
•
=1,
∴
=
,
又∵∠ACP=PCB=90°,
∴△ACP∽△PCB,
∴∠PAC=∠BPC,
∵∠PAC+∠APC=90°,
∴∠BPC+∠APC=90°,
即∠APB=90°,
∴△PAB是直角三角形;
(2)解:∵点A(-4,0),点B(6,0),点P的横坐标为-2,
∴AC=-2-(-4)=-2+4=2,
BC=6-(-2)=6+2=8,
∴
•
=1,
解得PC=4,
∴点P的坐标为(-2,-4),
设过P、A、B三个点的抛物线的表达式为y=a(x+4)(x-6),
将点P的坐标代入得,a(-2+4)(-2-6)=-4,
解得a=
,
所以,y=
(x+4)(x-6)=
(x2-2x-24)=
x2-
x-6,
所以,抛物线解析式为y=
x2-
x-6;
∵y=
x2-
x-6=
(x2-2x+1)-
-6=
(x-1)2-
,
∴顶点坐标为(1,-
).
∵tan∠PAB•tan∠PBA=1,
∴
| PC |
| AC |
| PC |
| BC |
∴
| PC |
| AC |
| BC |
| PC |
又∵∠ACP=PCB=90°,
∴△ACP∽△PCB,
∴∠PAC=∠BPC,
∵∠PAC+∠APC=90°,

∴∠BPC+∠APC=90°,
即∠APB=90°,
∴△PAB是直角三角形;
(2)解:∵点A(-4,0),点B(6,0),点P的横坐标为-2,
∴AC=-2-(-4)=-2+4=2,
BC=6-(-2)=6+2=8,
∴
| PC |
| 2 |
| PC |
| 8 |
解得PC=4,
∴点P的坐标为(-2,-4),
设过P、A、B三个点的抛物线的表达式为y=a(x+4)(x-6),
将点P的坐标代入得,a(-2+4)(-2-6)=-4,
解得a=
| 1 |
| 4 |
所以,y=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
所以,抛物线解析式为y=
| 1 |
| 4 |
| 1 |
| 2 |
∵y=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 25 |
| 4 |
∴顶点坐标为(1,-
| 25 |
| 4 |
点评:本题是二次函数综合题型,主要利用了锐角三角函数,相似三角形的判定与性质,待定系数法求二次函数解析式,二次函数的性质,(1)作辅助线构造出相似三角形并列出锐角的正切是解题的关键,(2)利用交点式解析式求解更简便.

练习册系列答案
相关题目
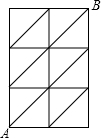 如图,在6个边长为1的小正方形及其部分对角线构成的图形中,如图从A点到B点只能沿图中的线段走,那么从A点到B点的最短距离为( )
如图,在6个边长为1的小正方形及其部分对角线构成的图形中,如图从A点到B点只能沿图中的线段走,那么从A点到B点的最短距离为( )| A、5 | ||
B、2
| ||
C、
| ||
D、
|
若m2+m-1=0,则m3+2m2+3等于( )
| A、2 | B、4 | C、-2 | D、-4 |
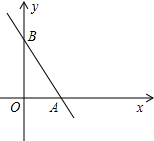 如图,y=kx+b的图象过点P(1,4),且与x轴、y轴的正半轴交于A、B,原点为O,问k、b为何值时,△AOB的面积最小?
如图,y=kx+b的图象过点P(1,4),且与x轴、y轴的正半轴交于A、B,原点为O,问k、b为何值时,△AOB的面积最小? 两个正方形如图所示装置,边长分别为m,n,求图阴影部分的面积.
两个正方形如图所示装置,边长分别为m,n,求图阴影部分的面积. 如图,点P、Q在数轴上表示的数分别是-8、4,点P以每秒2个单位的速度运动,点Q以每秒1个单位的速度运动.设点P、Q同时出发,运动时间为t秒.
如图,点P、Q在数轴上表示的数分别是-8、4,点P以每秒2个单位的速度运动,点Q以每秒1个单位的速度运动.设点P、Q同时出发,运动时间为t秒.