题目内容
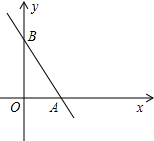 如图,y=kx+b的图象过点P(1,4),且与x轴、y轴的正半轴交于A、B,原点为O,问k、b为何值时,△AOB的面积最小?
如图,y=kx+b的图象过点P(1,4),且与x轴、y轴的正半轴交于A、B,原点为O,问k、b为何值时,△AOB的面积最小?考点:一次函数图象上点的坐标特征,二次函数的最值
专题:
分析:由条件可用k和b分别表示出OA和OB,从而表示出△OAB的面积,由条件得到k+b=4,代入消去b,再利用基本不等式求得其最小值.
解答:解:
令y=0可得x=-
,令x=0可得y=b,
∴OA=-
,OB=b,
∵图象过点P(1,4),
∴k+b=4,即b=4-k,
∴S△AOB=
OA•OB=-
=-
=-
-
+4,
由题知k<0,=-
>0,-
>0,且(-
)×(-
)=4,
∴=-
-
≥2
=4,
∴=-
-
+4≥4+4=8,
∴S△AOB≥8,
∴△AOB面积的最小值为8.
令y=0可得x=-
| b |
| k |
∴OA=-
| b |
| k |
∵图象过点P(1,4),
∴k+b=4,即b=4-k,
∴S△AOB=
| 1 |
| 2 |
| b2 |
| 2k |
| (4-k)2 |
| 2k |
| 8 |
| k |
| k |
| 2 |
由题知k<0,=-
| 8 |
| k |
| k |
| 2 |
| 8 |
| k |
| k |
| 2 |
∴=-
| 8 |
| k |
| k |
| 2 |
(-
|
∴=-
| 8 |
| k |
| k |
| 2 |
∴S△AOB≥8,
∴△AOB面积的最小值为8.
点评:本题主要考查一次函数图象上点的特征及基本不等式的应用,由条件用k或b表示出△AOB的面积是解题的关键.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
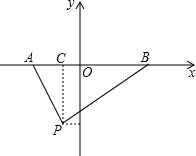 求如图,已知点A(-4,0)和点B(6,0),第三象限内有一点P,它的横坐标为-2,并且满足条件tan∠PAB•tan∠PBA=1.
求如图,已知点A(-4,0)和点B(6,0),第三象限内有一点P,它的横坐标为-2,并且满足条件tan∠PAB•tan∠PBA=1.