题目内容
 如图,点P、Q在数轴上表示的数分别是-8、4,点P以每秒2个单位的速度运动,点Q以每秒1个单位的速度运动.设点P、Q同时出发,运动时间为t秒.
如图,点P、Q在数轴上表示的数分别是-8、4,点P以每秒2个单位的速度运动,点Q以每秒1个单位的速度运动.设点P、Q同时出发,运动时间为t秒.(1)若点P、Q同时向右运动2秒,则点P表示的数为
(2)经过
(3)试探究:经过多少秒后,点P、Q两点间的距离为14个单位.
考点:数轴
专题:
分析:(1)根据数轴上的数向右移动加列式计算即可得解;用点Q运动的路程加上两数原来的距离再减去点P运动的距离计算即可得解;
(2)分相遇问题和追及问题两种情况分别列方程求解即可;
(3)分①点P向左,点Q向右移动,②点P、Q向右都向右移动,③点P、Q都向左移动,④点P向右,点Q向左移动分别列出方程,然后求解即可.
(2)分相遇问题和追及问题两种情况分别列方程求解即可;
(3)分①点P向左,点Q向右移动,②点P、Q向右都向右移动,③点P、Q都向左移动,④点P向右,点Q向左移动分别列出方程,然后求解即可.
解答:解:(1)点P表示的数为-8+2×2=-8+4=-4,
P、Q间的距离为:1×2+12-2×2=2+12-4=10;
(2)若相向而行,则2t+t=12,
解得t=4,
若点P、Q同向向右而行,则2t-t=12,
解得t=12,
综上所述,经过4或12秒后,点P、Q重合;
故答案为:(1)-4,10;(2)4或12;
(3)①点P向左,点Q向右移动,则2t+t+12=14,
解得t=
;
②点P、Q向右都向右移动,则2t-(t+12)=14,
解得t=26,
③点P、Q都向左移动,则2t+12-t=14,
解得t=2,
④点P向右,点Q向左移动,则2t+t=12+14,
解得t=
,
综上所述,经过
,26,2,
秒时,P、Q相距14个单位.
P、Q间的距离为:1×2+12-2×2=2+12-4=10;
(2)若相向而行,则2t+t=12,
解得t=4,
若点P、Q同向向右而行,则2t-t=12,
解得t=12,
综上所述,经过4或12秒后,点P、Q重合;
故答案为:(1)-4,10;(2)4或12;
(3)①点P向左,点Q向右移动,则2t+t+12=14,
解得t=
| 2 |
| 3 |
②点P、Q向右都向右移动,则2t-(t+12)=14,
解得t=26,
③点P、Q都向左移动,则2t+12-t=14,
解得t=2,
④点P向右,点Q向左移动,则2t+t=12+14,
解得t=
| 26 |
| 3 |
综上所述,经过
| 2 |
| 3 |
| 26 |
| 3 |
点评:本题考查了数轴,主要利用了数轴上两点间的距离的表示,数轴上的数向右移动加向左移动减,难点在于(3)分情况讨论.

练习册系列答案
相关题目
如果∠1和∠2是内错角,且∠1=40°,那么∠2为( )
| A、40° | B、50° |
| C、140° | D、不能确定 |
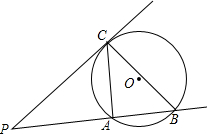 如图 P是⊙O外一点,过点P作直线PA与⊙O相交,交点为A、B,作直线PC与⊙O相切,切点为C,连接AC、AD.
如图 P是⊙O外一点,过点P作直线PA与⊙O相交,交点为A、B,作直线PC与⊙O相切,切点为C,连接AC、AD.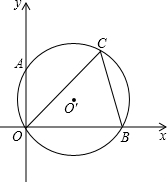 如图所示,已知CO、CB是⊙O′的弦,⊙O′与平面直角坐标系的x轴、y轴分别相交于点B、A,若∠COB=45°,∠OBC=75°,点A的坐标为(0,2),求⊙O′的直径.
如图所示,已知CO、CB是⊙O′的弦,⊙O′与平面直角坐标系的x轴、y轴分别相交于点B、A,若∠COB=45°,∠OBC=75°,点A的坐标为(0,2),求⊙O′的直径.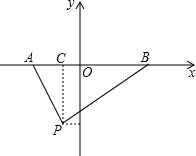 求如图,已知点A(-4,0)和点B(6,0),第三象限内有一点P,它的横坐标为-2,并且满足条件tan∠PAB•tan∠PBA=1.
求如图,已知点A(-4,0)和点B(6,0),第三象限内有一点P,它的横坐标为-2,并且满足条件tan∠PAB•tan∠PBA=1.