题目内容
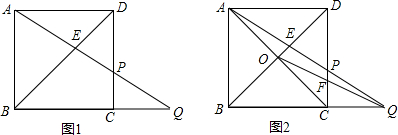
如图1,已知正方形ABCD边长为1,点Q为BC延长线上的一个动点,QA与CD、BD分别交于点P、E.
(1)当CQ=
时,求
的值;
(2)如图2,如果对角线AC与BD相交于点O,联结QO,交CD于点F,设CQ=x,S△EOQ=y,求y关于x的函数关系式,并求出x的取值范围;
(3)在(2)的条件下,△DEP能否与△DBQ相似,若能请求出x的值,若不能请说明理由.
(1)当CQ=
| 5 |
| 4 |
| QE |
| QA |
(2)如图2,如果对角线AC与BD相交于点O,联结QO,交CD于点F,设CQ=x,S△EOQ=y,求y关于x的函数关系式,并求出x的取值范围;
(3)在(2)的条件下,△DEP能否与△DBQ相似,若能请求出x的值,若不能请说明理由.

考点:相似形综合题
专题:
分析:(1)先求出BQ,再根据AD∥BQ得出
=
=
,即可求出
;
(2)作QH⊥BD,垂足为点H,根据∠DBQ=45°,得出QH=
(1+x),根据AD∥BQ,得出
=
,再求出DE=
,根据OD=
BD=
,求出OE,最后根据y=
OE•QH代入整理即可;
(3)先求出∠EDP=∠DBQ=45°,再根据若∠DEP=∠BDQ,则△DEP∽△BDQ,再求出∠AQC=∠1=∠2,证出△DAP≌△CQD,得出PC=1-x,再根据△ADP∽△QCP,得到
=
,得出
=
即可求出x的值.
| AE |
| QE |
| AD |
| BQ |
| 4 |
| 9 |
| QE |
| QA |
(2)作QH⊥BD,垂足为点H,根据∠DBQ=45°,得出QH=
| ||
| 2 |
| DE |
| EB |
| AD |
| BQ |
| ||
| 2+x |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
(3)先求出∠EDP=∠DBQ=45°,再根据若∠DEP=∠BDQ,则△DEP∽△BDQ,再求出∠AQC=∠1=∠2,证出△DAP≌△CQD,得出PC=1-x,再根据△ADP∽△QCP,得到
| AD |
| DP |
| CQ |
| PC |
| 1 |
| x |
| x |
| 1-x |
解答:解:(1)∵CQ=
,
∴BQ=BC+CQ=1+
=
,
∵AD∥BQ,
∴
=
=
,
∴
=
;
(2)作QH⊥BD,垂足为点H,
∵ABCD是正方形,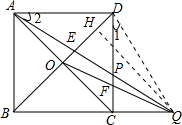
∴∠DBQ=45°,
在Rt△BQH中,QH=BQsin∠DBQ=
(1+x),
∵AD∥BQ,
∴
=
,
∵BD=
,
∴DE=
,
∵OD=
BD=
,
∴OE=OD-DE=
-
=
,
∴y=
OE•QH=
×
(1+x)×
=
(x>0);
(3)∵四边形ABCD是正方形,
∴∠EDP=∠DBQ=45°,
若∠DEP=∠BDQ,则△DEP∽△BDQ,∵∠DEP=∠DBQ+∠AQC,∠BDQ=∠BDC+∠1,
∴∠AQC=∠1=∠2,
在△DAP和△CQD中,
,
∴△DAP≌△CQD(ASA),
∴DP=CQ=x,
∴PC=1-x,
∵△ADP∽△QCP,
∴
=
,
∴
=
,
解得:x1=
,x2=
(舍去),
∴x的值是
.
| 5 |
| 4 |
∴BQ=BC+CQ=1+
| 5 |
| 4 |
| 9 |
| 4 |
∵AD∥BQ,
∴
| AE |
| QE |
| AD |
| BQ |
| 4 |
| 9 |
∴
| QE |
| QA |
| 9 |
| 13 |
(2)作QH⊥BD,垂足为点H,
∵ABCD是正方形,

∴∠DBQ=45°,
在Rt△BQH中,QH=BQsin∠DBQ=
| ||
| 2 |
∵AD∥BQ,
∴
| DE |
| EB |
| AD |
| BQ |
∵BD=
| 2 |
∴DE=
| ||
| 2+x |
∵OD=
| 1 |
| 2 |
| ||
| 2 |
∴OE=OD-DE=
| ||
| 2 |
| ||
| 2+x |
| ||
| 2(2+x) |
∴y=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2(2+x) |
| x(1+x) |
| 4(2+x) |
(3)∵四边形ABCD是正方形,
∴∠EDP=∠DBQ=45°,
若∠DEP=∠BDQ,则△DEP∽△BDQ,∵∠DEP=∠DBQ+∠AQC,∠BDQ=∠BDC+∠1,
∴∠AQC=∠1=∠2,
在△DAP和△CQD中,
|
∴△DAP≌△CQD(ASA),
∴DP=CQ=x,
∴PC=1-x,
∵△ADP∽△QCP,
∴
| AD |
| DP |
| CQ |
| PC |
∴
| 1 |
| x |
| x |
| 1-x |
解得:x1=
-1+
| ||
| 2 |
-1-
| ||
| 2 |
∴x的值是
-1+
| ||
| 2 |
点评:此题考查了相似形的综合,用到的知识点是正方形的性质、相似三角形和全等三角形的判定与性质,关键是根据题意作出辅助线,找出相似的三角形.

练习册系列答案
相关题目
 如图所示,数轴上A.B两点表示的数分别为
如图所示,数轴上A.B两点表示的数分别为| 3 |
A、
| ||
B、3-
| ||
C、3-2
| ||
D、2
|
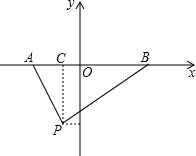 求如图,已知点A(-4,0)和点B(6,0),第三象限内有一点P,它的横坐标为-2,并且满足条件tan∠PAB•tan∠PBA=1.
求如图,已知点A(-4,0)和点B(6,0),第三象限内有一点P,它的横坐标为-2,并且满足条件tan∠PAB•tan∠PBA=1.