题目内容
17.在数轴上,与2$\sqrt{3}$相距5$\sqrt{3}$个单位长度的点所表示的数是-3$\sqrt{3}$或7$\sqrt{3}$.分析 分在表示2$\sqrt{3}$的数的左边与右边两种情况讨论求解.
解答 解:在2$\sqrt{3}$的左边时,2$\sqrt{3}$-5$\sqrt{3}$=-3$\sqrt{3}$,
在2$\sqrt{3}$的右边时,2$\sqrt{3}$+5$\sqrt{3}$=7$\sqrt{3}$,
所以,所表示的数是-3$\sqrt{3}$或7$\sqrt{3}$.
故答案为:-3$\sqrt{3}$或7$\sqrt{3}$.
点评 本题考查了实数与数轴,是基础题,难点在于要分两种情况讨论.

练习册系列答案
相关题目
8. 如图,已知直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是( )
如图,已知直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是( )
 如图,已知直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是( )
如图,已知直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是( )| A. | 10$\sqrt{3}$+1 | B. | 10$\sqrt{3}$ | C. | 10.5 | D. | 11.5 |
12.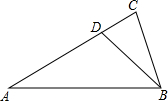 如图,∠A=∠CBD=30°,∠ABD=45°,则以下结论错误的是( )
如图,∠A=∠CBD=30°,∠ABD=45°,则以下结论错误的是( )
 如图,∠A=∠CBD=30°,∠ABD=45°,则以下结论错误的是( )
如图,∠A=∠CBD=30°,∠ABD=45°,则以下结论错误的是( )| A. | AB=3CD | B. | BC2=CD•AB | ||
| C. | △BCD是等腰三角形 | D. | 2CD=($\sqrt{3}-1$)AD |
9. 如图,AB⊥BD,ED⊥BD,垂足分别为B、D,则下列各式中正确的是( )
如图,AB⊥BD,ED⊥BD,垂足分别为B、D,则下列各式中正确的是( )
 如图,AB⊥BD,ED⊥BD,垂足分别为B、D,则下列各式中正确的是( )
如图,AB⊥BD,ED⊥BD,垂足分别为B、D,则下列各式中正确的是( )| A. | $\frac{EC}{AC}$=$\frac{BD}{DC}$ | B. | $\frac{AC}{AE}$=$\frac{BC}{DC}$ | C. | $\frac{EC}{BD}$=$\frac{AC}{DC}$ | D. | $\frac{AC}{EC}$=$\frac{BC}{DC}$ |
6.已知△ABC中,求作一点P,使P到∠A的两边的距离相等,且PB=PC,则下列确定P点的方法正确的是( )
| A. | P是∠A与∠B两角平分线的交点 | |
| B. | P是AC、AB两边上中垂线的交点 | |
| C. | P是∠A的角平分线与BC的中垂线的交点 | |
| D. | P是∠A的角平分线与AB的中垂线的交点 |
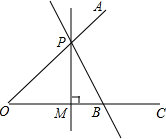 画图并回答问题.
画图并回答问题.