题目内容
12.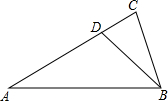 如图,∠A=∠CBD=30°,∠ABD=45°,则以下结论错误的是( )
如图,∠A=∠CBD=30°,∠ABD=45°,则以下结论错误的是( )| A. | AB=3CD | B. | BC2=CD•AB | ||
| C. | △BCD是等腰三角形 | D. | 2CD=($\sqrt{3}-1$)AD |
分析 根据已知条件得到∠ABC=75°,根据三角形的内角和得到∠C=180°-∠A-∠ABC=75°,于是得到△BCD是等腰三角形,故C正确;根据相似三角形的性质得到$\frac{BC}{CD}=\frac{AB}{BC}$,于是得到BC2=CD•AB,故B正确;过D作DE⊥AB于E,设DE=BE=x,解直角三角形得到AE=$\sqrt{3}$x,AD=2x,BC=BD=$\sqrt{2}$x,根据BC2=CD•AB,于是得到2CD=2($\sqrt{3}$-1)x=($\sqrt{3}$-1)•AD,故D正确;由于AD=2DE≠2CD,于是得到AB≠3CD,故A错误.
解答 解:∵∠A=∠CBD=30°,∠ABD=45°,
∴∠ABC=75°,
∴∠C=180°-∠A-∠ABC=75°,
∴∠ABC=∠C,
∴△BCD是等腰三角形;故C正确;
∵∠C=∠C,
∴△ABC∽△CBD,
∴$\frac{BC}{CD}=\frac{AB}{BC}$,
∴BC2=CD•AB,故B正确;
过D作DE⊥AB于E,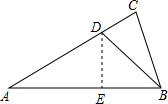 设DE=BE=x,
设DE=BE=x,
∴AE=$\sqrt{3}$x,AD=2x,BC=BD=$\sqrt{2}$x,
∵BC2=CD•AB,
∴($\sqrt{2}$x)2=CD•($\sqrt{3}$x+x)
∴CD=($\sqrt{3}$-1)x,
∴2CD=2($\sqrt{3}$-1)x=($\sqrt{3}$-1)•AD,故D正确;
∵AD=2DE≠2CD,
∴AB≠3CD,故A错误.
故选A.
点评 本题考查了相似三角形的判定和性质,等腰三角形的判定,解直角三角形,正确的作出辅助线是解题的关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
2. 如图所示,下列说法正确的是( )
如图所示,下列说法正确的是( )
 如图所示,下列说法正确的是( )
如图所示,下列说法正确的是( )| A. | ∠2与∠4是同旁内角 | B. | ∠1与∠4是内错角 | ||
| C. | ∠3与∠6是同位角 | D. | ∠2与∠5是同位角 |
20.下列说法正确的是( )
| A. | “黑色”和“白色”表示具有相反意义的量 | |
| B. | “快”和“慢”表示具有相反意义的量 | |
| C. | “向南100米”和“向北1000米”表示具有相反意义的量 | |
| D. | “+15米”就表示向东走了15米 |
 如图,已知Rt△ABC中,∠BAC=90°,∠ACB=30°.
如图,已知Rt△ABC中,∠BAC=90°,∠ACB=30°. 有理数m,n在数轴上的位置如图所示,那么化简|2m-2n|-$\sqrt{(n-m)^{2}}$的结果是m-n.
有理数m,n在数轴上的位置如图所示,那么化简|2m-2n|-$\sqrt{(n-m)^{2}}$的结果是m-n.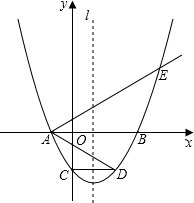 如图,已知二次函数y=m2x2-2mx-3(m是常数,m>0)的图象与x轴分别相交于点A、B(点A位于点B的左侧),与y轴交于点C,对称轴为直线l.点C关于l的对称点为D,连接AD.点E为该函数图象上一点,AB平分∠DAE.
如图,已知二次函数y=m2x2-2mx-3(m是常数,m>0)的图象与x轴分别相交于点A、B(点A位于点B的左侧),与y轴交于点C,对称轴为直线l.点C关于l的对称点为D,连接AD.点E为该函数图象上一点,AB平分∠DAE.