题目内容
12．
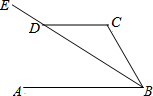如图：已知AB∥CD，BE平分∠ABC，∠CDE=140°，则∠C为（ ）| A． | 80° | B． | 105° | C． | 100° | D． | 110° |
分析 由∠CDE=140°，可求得其邻补角∠CDB的度数，然后由AB∥CD，根据平行线的性质，可求得∠ABD的度数，然后由BE平分∠ABC，可求得∠ABC的度数，继而求得答案．
解答 解：∵∠CDE=140°，
∴∠CDB=180°-∠CDE=40°，
∵AB∥CD，
∴∠ABD=∠CDB=40°，
∵BE平分∠ABC，
∴∠ABC=2∠ABD=80°，
∴∠C=180°-∠ABC=100°．
故选C．
点评 此题考查了平行线的性质．注意两直线平行，内错角相等，同旁内角互补定理的应用．
练习册系列答案
阅读快车系列答案
相关题目
2．
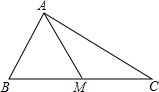如图，AM是△ABC的中线，若△ABM的面积为4，则△ABC的面积为（ ）
如图，AM是△ABC的中线，若△ABM的面积为4，则△ABC的面积为（ ）| A． | 2 | B． | 4 | C． | 6 | D． | 8 |
20．
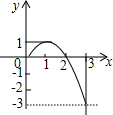已知二次函数y=ax2+bx+c（a≠0）（0≤x≤3）的图象如图所示，则该函数在所给自变量取值范围内，下列说法正确的是（ ）
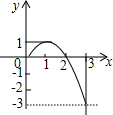已知二次函数y=ax2+bx+c（a≠0）（0≤x≤3）的图象如图所示，则该函数在所给自变量取值范围内，下列说法正确的是（ ）| A． | 有最大值1，没有最小值 | B． | 有最大值3，有最小值-3 | ||
| C． | 有最大值1，有最小值-3 | D． | 有最大值3，有最小值1 |
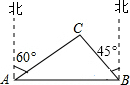我市某旗在棚户区改造工程中需要修建一段东西方向全长2000米的道路（记作AB）．已知C点周围700米范围内有一电力设施区域．在A处测得C在A的北偏东60°方向上，在B处测得C在B的北偏西45°方向上．（$\sqrt{3}$≈1.7，$\sqrt{2}$≈1.4）
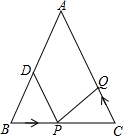如图所示，已知△ABC中，AB=AC=10厘米，BC=8厘米，点D为AB的中点．