题目内容
3.(1)计算:$|{-2}|+{(\sqrt{3}-1)^0}-{({\frac{1}{3}})^{-1}}-{(-1)^{2011}}$(2)计算:$\frac{3}{(x-1)^{2}}$-$\frac{3x}{(x-1)^{2}}$
(3)化简:$\frac{{a}^{3}}{3c}$÷$\frac{a{b}^{2}}{{c}^{2}}$•($\frac{-3{b}^{2}}{ac}$)2.
分析 (1)原式第一项利用绝对值的代数意义化简,第二项利用零指数幂法则计算,第三项利用负整数指数幂法则计算,最后一项利用乘方的意义化简即可得到结果;
(2)原式利用同分母分式的减法法则计算即可得到结果;
(3)原式先计算乘方运算,再计算乘除运算即可得到结果.
解答 解:(1)原式=2+1-3+1=1;
(2)原式=$\frac{3-3x}{(x-1)^{2}}$=$\frac{-3(x-1)}{(x-1)^{2}}$=-$\frac{3}{x-1}$;
(3)原式=$\frac{{a}^{3}}{3c}$•$\frac{{c}^{2}}{a{b}^{2}}$•$\frac{9{b}^{4}}{{a}^{2}{c}^{2}}$=$\frac{3{b}^{2}}{c}$.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
11.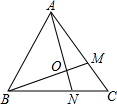 在等边△ABC中,M是AC上一点,N是BC上的一点,且AM=BN,∠MBC=25°,AN与BM交于点O,则∠MON的度数为( )
在等边△ABC中,M是AC上一点,N是BC上的一点,且AM=BN,∠MBC=25°,AN与BM交于点O,则∠MON的度数为( )
 在等边△ABC中,M是AC上一点,N是BC上的一点,且AM=BN,∠MBC=25°,AN与BM交于点O,则∠MON的度数为( )
在等边△ABC中,M是AC上一点,N是BC上的一点,且AM=BN,∠MBC=25°,AN与BM交于点O,则∠MON的度数为( )| A. | 110° | B. | 105° | C. | 90° | D. | 85° |
18.某里弄所有的263户家庭人口数分组表示如下:
计算总体均值μ,中位数m,方差s2和标准差s.
| 家庭人口数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 家庭数 | 20 | 29 | 48 | 50 | 46 | 36 | 19 | 8 | 4 | 3 |
8.下列各式计算正确的是( )
| A. | $\sqrt{(-9)(-4)}=\sqrt{-9}•\sqrt{-4}=(-3)(-2)=6$ | B. | $\sqrt{8}-\sqrt{2}=\sqrt{2}$ | ||
| C. | $\sqrt{{3^2}+{4^2}}=3+4=7$ | D. | $\frac{{6-\sqrt{2}}}{{\sqrt{2}}}=3\sqrt{2}$ |
15.学校总务处与教务处各领了同样数量的信封和信笺,总务处每发出一封信都只用1张信笺,教务处每发出一封信都用3张信笺,结果,总务处用掉了所有的信封,但余下50张信笺;而教务处用掉了所有信笺,但余下50个信封.则两处所领的信笺张数、信封个数分别为( )
| A. | 150,100 | B. | 125,75 | C. | 120,70 | D. | 100,150 |
12.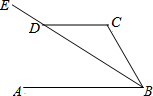 如图:已知AB∥CD,BE平分∠ABC,∠CDE=140°,则∠C为( )
如图:已知AB∥CD,BE平分∠ABC,∠CDE=140°,则∠C为( )
 如图:已知AB∥CD,BE平分∠ABC,∠CDE=140°,则∠C为( )
如图:已知AB∥CD,BE平分∠ABC,∠CDE=140°,则∠C为( )| A. | 80° | B. | 105° | C. | 100° | D. | 110° |
 如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠A-∠P=30°.
如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠A-∠P=30°.