题目内容
2.关于x的方程mx2-(2m+1)x+m=0有两个实根,则实数m的取值范围是m≥-$\frac{1}{4}$且m≠0.分析 根据方程有两个实数根,得到根的判别式大于等于0,列出关于m的不等式,求出不等式的解集,即可得到m的范围.
解答 解:∵关于x的方程mx2-(2m-1)x+m-2=0有两个实数根,
∴△=b2-4ac=(2m+1) 2-4m•m≥0,
解得:m≥-$\frac{1}{4}$,
则m的取值范围是m≥-$\frac{1}{4}$且m≠0.
故答案为:m≥-$\frac{1}{4}$且m≠0.
点评 此题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的判别式△=b2-4ac.当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程没有实数根.同时考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的定义.

练习册系列答案
相关题目
12.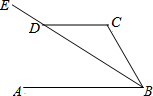 如图:已知AB∥CD,BE平分∠ABC,∠CDE=140°,则∠C为( )
如图:已知AB∥CD,BE平分∠ABC,∠CDE=140°,则∠C为( )
 如图:已知AB∥CD,BE平分∠ABC,∠CDE=140°,则∠C为( )
如图:已知AB∥CD,BE平分∠ABC,∠CDE=140°,则∠C为( )| A. | 80° | B. | 105° | C. | 100° | D. | 110° |
10.菱形ABCD的两条对角线AC=6,BD=4,则$sin\frac{A}{2}$的值是( )
| A. | $\frac{5}{13}$ | B. | $\frac{5}{12}$ | C. | $\frac{{3\sqrt{13}}}{13}$ | D. | $\frac{{2\sqrt{13}}}{13}$ |
14.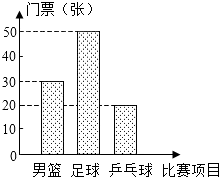 下表为抄录北京奥运会官方票务网公布的三种球类比赛的部分门票价格,某公司购买的门票种类、数量绘制的条形统计图如图.
下表为抄录北京奥运会官方票务网公布的三种球类比赛的部分门票价格,某公司购买的门票种类、数量绘制的条形统计图如图.
依据上列图、表,回答下列问题:
(1)其中观看男篮比赛的门票有30 张;观看乒乓球比赛的门票占全部门票的20%;
(2)公司决定采用随机抽取的方式把门票分配给100名员工,在看不到门票的条件下,每人抽取一张(假设所有的门票形状、大小、质地等完全相同且充分洗匀),问员工小亮抽到足球门票的概率是$\frac{1}{2}$;
(3)若购买乒乓球门票的总款数占全部门票总款数的$\frac{1}{8}$,试求每张乒乓球门票的价格.
 下表为抄录北京奥运会官方票务网公布的三种球类比赛的部分门票价格,某公司购买的门票种类、数量绘制的条形统计图如图.
下表为抄录北京奥运会官方票务网公布的三种球类比赛的部分门票价格,某公司购买的门票种类、数量绘制的条形统计图如图.| 比赛项目 | 票价(元/张) |
| 男 篮 | 1000 |
| 足 球 | 800 |
| 乒乓球 | x |
(1)其中观看男篮比赛的门票有30 张;观看乒乓球比赛的门票占全部门票的20%;
(2)公司决定采用随机抽取的方式把门票分配给100名员工,在看不到门票的条件下,每人抽取一张(假设所有的门票形状、大小、质地等完全相同且充分洗匀),问员工小亮抽到足球门票的概率是$\frac{1}{2}$;
(3)若购买乒乓球门票的总款数占全部门票总款数的$\frac{1}{8}$,试求每张乒乓球门票的价格.
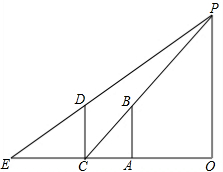 晚上,一个身高1.6米的人站在路灯下,发现自己的影子刚好是4块地砖的长(地砖是边长为0.5米的正方形),当他沿着影子的方向走了4块地砖时,发现自己的影子刚好是5块地砖的长,根据他的发现,你能不能计算路灯的高度?
晚上,一个身高1.6米的人站在路灯下,发现自己的影子刚好是4块地砖的长(地砖是边长为0.5米的正方形),当他沿着影子的方向走了4块地砖时,发现自己的影子刚好是5块地砖的长,根据他的发现,你能不能计算路灯的高度?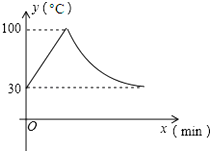 教室里的饮水机接通电源就进入加热程序,水温每分钟上升10℃,加热到100℃时自动关机,水温开始下降,此时水温(℃)与时间(min)成反比例关系.若室温恒定为30℃,当水温降至30℃时,又启动第二轮加热程序.某轮加热过程中水温y(℃)和时间x(min)的关系如图所示.
教室里的饮水机接通电源就进入加热程序,水温每分钟上升10℃,加热到100℃时自动关机,水温开始下降,此时水温(℃)与时间(min)成反比例关系.若室温恒定为30℃,当水温降至30℃时,又启动第二轮加热程序.某轮加热过程中水温y(℃)和时间x(min)的关系如图所示.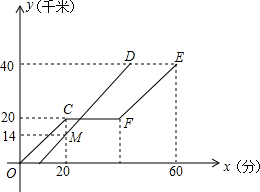 我市某路公汽每天匀速往返于停车场A和停车场B之间,每车次一般都按规定时间发车到站,如图是紧挨前后的甲乙两车从A出发的行驶路程y(千米)和甲车行驶时间x(分)的关系图,甲行驶20分钟因故障停车修理,乙车接到通知后加速赶到出事地点接走乘客,并按甲车预定时间把乘客送达终点,其他车辆按预定时间不变,甲车排除故障后也按原来速度继续行驶(乘客上下车时间不计)
我市某路公汽每天匀速往返于停车场A和停车场B之间,每车次一般都按规定时间发车到站,如图是紧挨前后的甲乙两车从A出发的行驶路程y(千米)和甲车行驶时间x(分)的关系图,甲行驶20分钟因故障停车修理,乙车接到通知后加速赶到出事地点接走乘客,并按甲车预定时间把乘客送达终点,其他车辆按预定时间不变,甲车排除故障后也按原来速度继续行驶(乘客上下车时间不计)