��Ŀ����
1��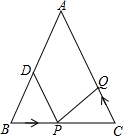 ��ͼ��ʾ����֪��ABC�У�AB=AC=10���ף�BC=8���ף���DΪAB���е㣮
��ͼ��ʾ����֪��ABC�У�AB=AC=10���ף�BC=8���ף���DΪAB���е㣮 ��1�������P���߶�BC����1����/����ٶ���B����C���˶���ͬʱ��Q���߶�CA����C����A���˶���
������Q���˶��ٶ����P���˶��ٶ���ȣ�����3���BPD���CQP�Ƿ�ȫ�ȣ���˵�����ɣ�
������Q���˶��ٶ����P���˶��ٶȲ���ȣ�����Q���˶��ٶ�Ϊ����ʱ���ܹ�ʹ��BPD���CQPȫ�ȣ�
��2������Q�ԣ�1�����е��˶��ٶȴӵ�C��������P��ԭ�����˶��ٶȴӵ�Bͬʱ����������ʱ���ء�ABC�����˶������ʱ���P���Q��һ���ڡ�ABC����������������
���� ��1���������BP=CQ=3��PC=BD=5��Ȼ����ݵȱ߶ԵȽ���á�B=��C��������SAS����֤����
����ΪVP��VQ������BP��CQ���֡�B=��C��Ҫʹ��BPD���CQPȫ�ȣ�ֻ��BP=CP=4������ȫ�ȵó�CQ=BD=5��Ȼ������˶��ٶ�����˶�ʱ�䣬����ʱ���CQ�ij��������Q���˶��ٶȣ�
��2����ΪVQ��VP��ֻ���ǵ�Q�ϵ�P������Q�ȵ�P����AB+AC��·�̣��ݴ��г����̣���������̼�����ã�
��� �⣺��1���١�t=3���룩��
��BP=CQ=3�����ף�
��AB=10��DΪAB�е㣬
��BD=5�����ף�
�֡�PC=BC-BP=8-3=5�����ף�
��PC=BD
��AB=AC��
���B=��C��
�ڡ�BPD���CQP�У�
$\left\{\begin{array}{l}{BP=CQ}\\{��B=��C}\\{BD=PC}\end{array}\right.$��
���BPD�ա�CQP��SAS����
�ڡ�VP��VQ��
��BP��CQ��
�֡ߡ�B=��C��
Ҫʹ��BPD�ա�CPQ��ֻ��BP=CP=4��
�ߡ�BPD�ա�CPQ��
��CQ=BD=5��
���P���˶�ʱ��t=$\frac{BP}{1}$=4���룩��
��ʱVQ=$\frac{CQ}{4}=\frac{5}{4}$=1.25������/�룩��
��2����ΪVQ��VP��ֻ���ǵ�Q�ϵ�P������Q�ȵ�P����AB+AC��·��
�辭��x���P��Q��һ���������������1.25x=x+2��10��
���x=80���룩��
��ʱP�˶���80��1=80�����ף���
�֡ߡ�ABC���ܳ�Ϊ28���ף�80=28��2+24��
���P��Q��AB������������������80�룬��P���Q��һ����AB����������
���� ���⿼����������ȫ�ȵ��ж������ʣ����������ε����ʣ��Լ����ν��˼������ã�����ĸ�������������������ȫ�ȵ��ж������ʣ�

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�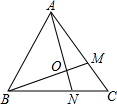 �ڵȱߡ�ABC�У�M��AC��һ�㣬N��BC�ϵ�һ�㣬��AM=BN����MBC=25�㣬AN��BM���ڵ�O�����MON�Ķ���Ϊ��������
�ڵȱߡ�ABC�У�M��AC��һ�㣬N��BC�ϵ�һ�㣬��AM=BN����MBC=25�㣬AN��BM���ڵ�O�����MON�Ķ���Ϊ��������| A�� | 110�� | B�� | 105�� | C�� | 90�� | D�� | 85�� |
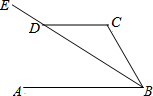 ��ͼ����֪AB��CD��BEƽ�֡�ABC����CDE=140�㣬���CΪ��������
��ͼ����֪AB��CD��BEƽ�֡�ABC����CDE=140�㣬���CΪ��������| A�� | 80�� | B�� | 105�� | C�� | 100�� | D�� | 110�� |
| A�� | ��x3��n+1 | B�� | ��xn+1��3 | C�� | x3•xn•x | D�� | x•x3n |
| A�� | 2-a | B�� | -2-a | C�� | $\frac{1}{2-a}$ | D�� | $-\frac{1}{2+a}$ |
| A�� | $\frac{5}{13}$ | B�� | $\frac{5}{12}$ | C�� | $\frac{{3\sqrt{13}}}{13}$ | D�� | $\frac{{2\sqrt{13}}}{13}$ |
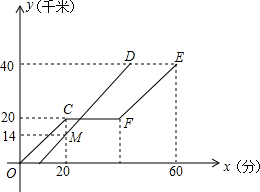 ����ij·����ÿ������������ͣ����A��ͣ����B֮�䣬ÿ����һ�㶼���涨ʱ�䷢����վ����ͼ�ǽ���ǰ��ļ���������A��������ʻ·��y��ǧ�ף��ͼ׳���ʻʱ��x���֣��Ĺ�ϵͼ������ʻ20���������ͣ���������ҳ��ӵ�֪ͨ����ٸϵ����µص���߳˿ͣ������׳�Ԥ��ʱ��ѳ˿��ʹ��յ㣬����������Ԥ��ʱ�䲻�䣬�׳��ų����Ϻ�Ҳ��ԭ���ٶȼ�����ʻ���˿����³�ʱ�䲻�ƣ�
����ij·����ÿ������������ͣ����A��ͣ����B֮�䣬ÿ����һ�㶼���涨ʱ�䷢����վ����ͼ�ǽ���ǰ��ļ���������A��������ʻ·��y��ǧ�ף��ͼ׳���ʻʱ��x���֣��Ĺ�ϵͼ������ʻ20���������ͣ���������ҳ��ӵ�֪ͨ����ٸϵ����µص���߳˿ͣ������׳�Ԥ��ʱ��ѳ˿��ʹ��յ㣬����������Ԥ��ʱ�䲻�䣬�׳��ų����Ϻ�Ҳ��ԭ���ٶȼ�����ʻ���˿����³�ʱ�䲻�ƣ�