题目内容
20．
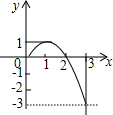已知二次函数y=ax2+bx+c（a≠0）（0≤x≤3）的图象如图所示，则该函数在所给自变量取值范围内，下列说法正确的是（ ）| A． | 有最大值1，没有最小值 | B． | 有最大值3，有最小值-3 | ||
| C． | 有最大值1，有最小值-3 | D． | 有最大值3，有最小值1 |
分析 直接根据函数的图象顶点坐标及最低点求出该函数在所给自变量的取值范围内的最大及最小值即可．
解答 解：由函数图象可知，此函数的顶点坐标为（1，1），
∵此抛物线开口向下，
∴此函数有最大值，最大值为1；
∵0≤x≤3，
∴当x=3时，函数最小值为-3．
故选：C．
点评 本题考查的是二次函数的最值及二次函数的图象，解答此题时要注意应用数形结合的思想求解．
练习册系列答案
相关题目
11．
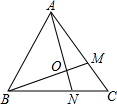在等边△ABC中，M是AC上一点，N是BC上的一点，且AM=BN，∠MBC=25°，AN与BM交于点O，则∠MON的度数为（ ）
在等边△ABC中，M是AC上一点，N是BC上的一点，且AM=BN，∠MBC=25°，AN与BM交于点O，则∠MON的度数为（ ）| A． | 110° | B． | 105° | C． | 90° | D． | 85° |
8．下列各式计算正确的是（ ）
| A． | $\sqrt{（-9）（-4）}=\sqrt{-9}•\sqrt{-4}=（-3）（-2）=6$ | B． | $\sqrt{8}-\sqrt{2}=\sqrt{2}$ | ||
| C． | $\sqrt{{3^2}+{4^2}}=3+4=7$ | D． | $\frac{{6-\sqrt{2}}}{{\sqrt{2}}}=3\sqrt{2}$ |
15．学校总务处与教务处各领了同样数量的信封和信笺，总务处每发出一封信都只用1张信笺，教务处每发出一封信都用3张信笺，结果，总务处用掉了所有的信封，但余下50张信笺；而教务处用掉了所有信笺，但余下50个信封．则两处所领的信笺张数、信封个数分别为（ ）
| A． | 150，100 | B． | 125，75 | C． | 120，70 | D． | 100，150 |
12．
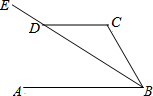如图：已知AB∥CD，BE平分∠ABC，∠CDE=140°，则∠C为（ ）
如图：已知AB∥CD，BE平分∠ABC，∠CDE=140°，则∠C为（ ）| A． | 80° | B． | 105° | C． | 100° | D． | 110° |
9．下列各式中与x3n+1相等的是（ ）
| A． | （x3）n+1 | B． | （xn+1）3 | C． | x3•xn•x | D． | x•x3n |
10．菱形ABCD的两条对角线AC=6，BD=4，则$sin\frac{A}{2}$的值是（ ）
| A． | $\frac{5}{13}$ | B． | $\frac{5}{12}$ | C． | $\frac{{3\sqrt{13}}}{13}$ | D． | $\frac{{2\sqrt{13}}}{13}$ |