题目内容
3.在△ABC中,BC=8,AB=x,AC=y,且x,y是二元一次方程3x+2y=20的正整数解,求所有满足条件的x和y的值.分析 先将x看做已知数求出y,即可确定出正整数解,再根据三角形三边关系求得结果.
解答 解:方程3x+2y=20变形,得:y=$\frac{20-3x}{2}$,
当x=2时,y=7;当x=4时,y=4;当x=6时,y=1;
∴方程3x+2y=20的正整数解为:$\left\{\begin{array}{l}{x=2}\\{y=7}\end{array}\right.$,$\left\{\begin{array}{l}{x=4}\\{y=4}\end{array}\right.$,$\left\{\begin{array}{l}{x=6}\\{y=1}\end{array}\right.$,
∵△ABC中,BC=8,AB=x,AC=y,
∴|x-y|<8,|x+y|>8,
∴$\left\{\begin{array}{l}{x=6}\\{y=1}\end{array}\right.$.
点评 此题考查了解二元一次方程,三角形三边关系,解题的关键是将x看做已知数求出y.

练习册系列答案
相关题目
13.∠α与∠β的度数分别是 2m-67和 68-m,且∠α与∠β都是∠γ 的补角,那么∠α与∠β的关系是( )
| A. | 互余但不相等 | B. | 互为补角 | C. | 相等但不互余 | D. | 互余且相等 |
10.下列计算正确的是( )
| A. | (2x2)3=2x5 | B. | $\sqrt{6}$÷$\sqrt{3}$=2 | C. | 3a2+2a=5a3 | D. | 2m•5n=10mn |
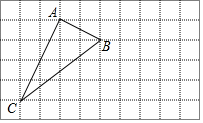 如图是一个6×10的正方形网格,点A,B,C都在格点上,sinB=$\frac{2\sqrt{5}}{5}$,在图中,使得△DBC为等腰三角形(BC为腰)的格点D的个数是8.
如图是一个6×10的正方形网格,点A,B,C都在格点上,sinB=$\frac{2\sqrt{5}}{5}$,在图中,使得△DBC为等腰三角形(BC为腰)的格点D的个数是8. 如图,已知抛物线y=ax2+bx(a≠0)经过A(4,4)、B(2,-2)两点,与x轴交于点C.
如图,已知抛物线y=ax2+bx(a≠0)经过A(4,4)、B(2,-2)两点,与x轴交于点C.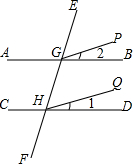 如图,已知GP平分∠EGB,HQ平分∠GHD,如果∠1=∠2,那么GP∥HQ吗?为什么?
如图,已知GP平分∠EGB,HQ平分∠GHD,如果∠1=∠2,那么GP∥HQ吗?为什么? 如图,AD是BC边上的高,AE平分∠BAC,∠B=60°,∠C=40°,求∠DAE的度数.
如图,AD是BC边上的高,AE平分∠BAC,∠B=60°,∠C=40°,求∠DAE的度数.