题目内容
11.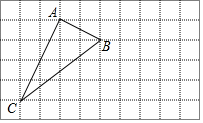 如图是一个6×10的正方形网格,点A,B,C都在格点上,sinB=$\frac{2\sqrt{5}}{5}$,在图中,使得△DBC为等腰三角形(BC为腰)的格点D的个数是8.
如图是一个6×10的正方形网格,点A,B,C都在格点上,sinB=$\frac{2\sqrt{5}}{5}$,在图中,使得△DBC为等腰三角形(BC为腰)的格点D的个数是8.
分析 根据勾股定理逆定理可判定△ABC为直角三角形,再由三角函数的定义可得sinB,分别以点C和点B为圆心、5为半径作圆可得格点D个数.
解答 解:∵AB2=12+22=5,AC2=22+42=20,BC2=32+52=25,
∴AB2+AC2=BC2,
则△ABC为直角三角形,且∠BAC=90°,
∴sinB=$\frac{AC}{BC}$=$\frac{2\sqrt{5}}{5}$,
如图,分别以点C和点B为圆心、5为半径作圆,
∴使得△DBC为等腰三角形(BC为腰)的格点D有8个,
故答案为:$\frac{2\sqrt{5}}{5}$,8.
点评 本题主要考查解直角三角形和等腰三角形的判定,熟练掌握勾股定理逆定理及等腰三角形的判定是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
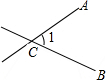
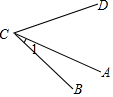
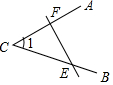
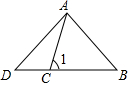
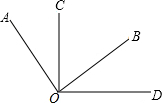 如图,∠AOB=∠COD=90°
如图,∠AOB=∠COD=90°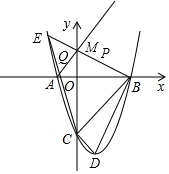 如图,抛物线y=x2+2ax+3a与x轴交于点A,B(点A在点B左侧),与y轴的负半轴交于点C,顶点为D,且OB=OC.
如图,抛物线y=x2+2ax+3a与x轴交于点A,B(点A在点B左侧),与y轴的负半轴交于点C,顶点为D,且OB=OC.