题目内容
2.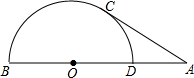 如图,点D为定线段AB上一动点,以BD为直径作半圆O,过A作半圆O的切线,切点为C,连CD,当(AC-AD)取最大值时,tan∠ACD=( )
如图,点D为定线段AB上一动点,以BD为直径作半圆O,过A作半圆O的切线,切点为C,连CD,当(AC-AD)取最大值时,tan∠ACD=( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
分析 连接BC、CD,首先证明ACD∽△ABC,AC2=AB•AD,设AB=K,AC=x,则AD=$\frac{{x}^{2}}{k}$,由二次函数的性质可知x=$\frac{K}{2}$时,AC-AD有最大值,由锐角三角函数的定义和相似三角形的性质求解即可.
解答 解:如图所示;连接BC、CD.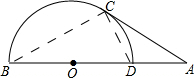
∵AC是圆O的切线,
∴∠ACD=∠CBD.
又∵∠A=∠A,
∴△ACD∽△ABC.
∴AC2=AB•AD,$\frac{AC}{AB}=\frac{CD}{BC}$.
设AB=k,AC=x,则AD=$\frac{{x}^{2}}{k}$.
∴AC-AD=$-\frac{{x}^{2}}{k}+x$.
由二次函数的性质可知:当x=-$\frac{b}{2a}=-\frac{1}{-\frac{1}{k}×2}=\frac{k}{2}$时,AC-AD有最大值.
即AC=$\frac{AB}{2}$时,AC-AD有最大值.
∴tan∠DCA=tan∠CBD=$\frac{CD}{BC}=\frac{1}{2}$.
故选:B.
点评 本题主要考查的切线的性质、相似三角形的性质和判定、二次函数的最值,根据题意列出AC-AD关于x的函数关系式是解题的关键.

练习册系列答案
相关题目
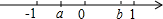 表示实数a,b的点在数轴上的位置如图所示,化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$+|b-a|.
表示实数a,b的点在数轴上的位置如图所示,化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$+|b-a|.
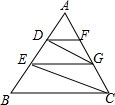 如图,DF∥EG,DG∥EC,DF∥BC,求证:AD:AE=AE:AB.
如图,DF∥EG,DG∥EC,DF∥BC,求证:AD:AE=AE:AB.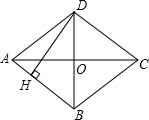 如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于点H,则DH=$\frac{24}{5}$.
如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于点H,则DH=$\frac{24}{5}$.