题目内容
3.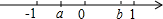 表示实数a,b的点在数轴上的位置如图所示,化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$+|b-a|.
表示实数a,b的点在数轴上的位置如图所示,化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$+|b-a|.
分析 先由数轴确定a,b的取值范围,根据差的绝对值是大数减小数,可化简绝对值,根据二次根式的性质,可化简二次根式.
解答 解:由数轴可得:a<0<b,
∴b-a>0,
$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$+|b-a|
=-a-b+b-a
=-2a.
点评 本题考查了实数与数轴,二次根式的性质与化简,利用了二次根式的性质,绝对值的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.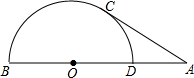 如图,点D为定线段AB上一动点,以BD为直径作半圆O,过A作半圆O的切线,切点为C,连CD,当(AC-AD)取最大值时,tan∠ACD=( )
如图,点D为定线段AB上一动点,以BD为直径作半圆O,过A作半圆O的切线,切点为C,连CD,当(AC-AD)取最大值时,tan∠ACD=( )
 如图,点D为定线段AB上一动点,以BD为直径作半圆O,过A作半圆O的切线,切点为C,连CD,当(AC-AD)取最大值时,tan∠ACD=( )
如图,点D为定线段AB上一动点,以BD为直径作半圆O,过A作半圆O的切线,切点为C,连CD,当(AC-AD)取最大值时,tan∠ACD=( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
3. 如图,直线AB、CD相交于点O,∠AOD与∠BOC的和为264°,那么∠AOC的度数是( )
如图,直线AB、CD相交于点O,∠AOD与∠BOC的和为264°,那么∠AOC的度数是( )
 如图,直线AB、CD相交于点O,∠AOD与∠BOC的和为264°,那么∠AOC的度数是( )
如图,直线AB、CD相交于点O,∠AOD与∠BOC的和为264°,那么∠AOC的度数是( )| A. | 58° | B. | 132° | C. | 48° | D. | 46° |
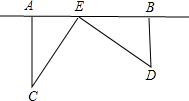 为了丰富少年儿童的业余生活,某社区要在如图中的AB所在的直线上建一图书室,本社区有两所学校所在的位置在点C和点D处,CA⊥AB于A,DB⊥AB于B.已知AB=2.5km,CA=1.5km,DB=1.0km,试问:图书室E应该建在距点A多少km处,才能使它到两所学校的距离相等?
为了丰富少年儿童的业余生活,某社区要在如图中的AB所在的直线上建一图书室,本社区有两所学校所在的位置在点C和点D处,CA⊥AB于A,DB⊥AB于B.已知AB=2.5km,CA=1.5km,DB=1.0km,试问:图书室E应该建在距点A多少km处,才能使它到两所学校的距离相等?