题目内容
2．若m是方程x2+2x-1=0的一个根，则代数式m3+3m2+m-5的值为-4．分析 根据一元二次方程的解的定义，将x=m代入已知方程求得m2+2m-1=0；然后将所求的代数式转化为含有（m2+2m-1）的代数式，并代入求值即可．
解答 解：根据题意，得
m2+2m-1=0，
则m3+3m2+m-5=（m2+2m-1）（m-1）-4=0-4=-4．
故答案是：-4．
点评 本题主要考查了方程的解的定义．此类题型的特点是：利用方程解的定义找到相等关系，再把所求的代数式化简后整理出所找到的相等关系的形式，再把此相等关系整体代入所求代数式，即可求出代数式的值．
练习册系列答案
阅读快车系列答案
相关题目
12．在实数0，-$\sqrt{2}$，-$\frac{2}{3}$，|-1|中，最小的数是（ ）
| A． | -$\frac{2}{3}$ | B． | -$\sqrt{2}$ | C． | 0 | D． | |-1| |
7．对于竖直向上抛出的物体，物体上升的高度h（m），初速度v（m/s）及抛出后经过的时间t（s）满足公式h=vt-5t2．若将一物体以25m/s的初速度向上抛，则多长时间后他在离出发点20m高的地方？
2．
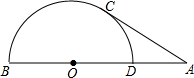如图，点D为定线段AB上一动点，以BD为直径作半圆O，过A作半圆O的切线，切点为C，连CD，当（AC-AD）取最大值时，tan∠ACD=（ ）
如图，点D为定线段AB上一动点，以BD为直径作半圆O，过A作半圆O的切线，切点为C，连CD，当（AC-AD）取最大值时，tan∠ACD=（ ）| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{\sqrt{3}}{3}$ |