题目内容
11.下列五个等式中一定成立的有( )①${(\sqrt{a})^2}=a$;②$\sqrt{a^2}=a$;③$\sqrt{a^4}={a^2}$;④a0=1;⑤$\sqrt{4\frac{1}{9}}=2\frac{1}{3}$.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 依据二次根式的性质和零指数幂的性质进行判断即可.
解答 解:①${(\sqrt{a})^2}=a$的条件是a≥0,故①不一定成立;
②当a<0时,$\sqrt{a^2}=a$不成立,故②不一定成立;
③$\sqrt{a^4}={a^2}$一定成立;
④a0=1的条件是a不等于0,故④不一定成立;
⑤$\sqrt{4\frac{1}{9}}$=$\sqrt{\frac{37}{9}}$=$\frac{\sqrt{37}}{3}$,故⑤错误.
故选:A.
点评 本题主要考查的是二次根式的性质、零指数幂的性质,熟记二次根式的性质、零指数幂的性质是解题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
2.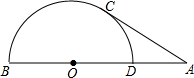 如图,点D为定线段AB上一动点,以BD为直径作半圆O,过A作半圆O的切线,切点为C,连CD,当(AC-AD)取最大值时,tan∠ACD=( )
如图,点D为定线段AB上一动点,以BD为直径作半圆O,过A作半圆O的切线,切点为C,连CD,当(AC-AD)取最大值时,tan∠ACD=( )
 如图,点D为定线段AB上一动点,以BD为直径作半圆O,过A作半圆O的切线,切点为C,连CD,当(AC-AD)取最大值时,tan∠ACD=( )
如图,点D为定线段AB上一动点,以BD为直径作半圆O,过A作半圆O的切线,切点为C,连CD,当(AC-AD)取最大值时,tan∠ACD=( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
6.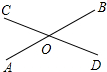 如图,直线AB与CD相交于点O,若∠AOC=$\frac{1}{3}$∠AOD,则∠BOD的度数为( )
如图,直线AB与CD相交于点O,若∠AOC=$\frac{1}{3}$∠AOD,则∠BOD的度数为( )
 如图,直线AB与CD相交于点O,若∠AOC=$\frac{1}{3}$∠AOD,则∠BOD的度数为( )
如图,直线AB与CD相交于点O,若∠AOC=$\frac{1}{3}$∠AOD,则∠BOD的度数为( )| A. | 30° | B. | 45° | C. | 60° | D. | 135° |
3. 如图,直线AB、CD相交于点O,∠AOD与∠BOC的和为264°,那么∠AOC的度数是( )
如图,直线AB、CD相交于点O,∠AOD与∠BOC的和为264°,那么∠AOC的度数是( )
 如图,直线AB、CD相交于点O,∠AOD与∠BOC的和为264°,那么∠AOC的度数是( )
如图,直线AB、CD相交于点O,∠AOD与∠BOC的和为264°,那么∠AOC的度数是( )| A. | 58° | B. | 132° | C. | 48° | D. | 46° |
1.已知关于x的方程kx2+(k+1)x+$\frac{k}{4}$=0有两个不相等的实数根,则k的取值范围( )
| A. | k=-$\frac{1}{2}$ | B. | k<-$\frac{1}{2}$ | C. | k≤-$\frac{1}{2}$ | D. | k>-$\frac{1}{2}$且k≠0 |
 如图,已知AB∥CD,∠1=∠2,求证:BE∥GF.
如图,已知AB∥CD,∠1=∠2,求证:BE∥GF.