题目内容
14.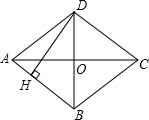 如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于点H,则DH=$\frac{24}{5}$.
如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于点H,则DH=$\frac{24}{5}$.
分析 先根据菱形的性质得OA=OC=4,OB=OD=3,AC⊥BD,再利用勾股定理计算出AB=5,然后根据菱形的面积公式得到$\frac{1}{2}$•AC•BD=DH•AB,再解关于DH的方程即可.
解答 解:∵四边形ABCD是菱形,
∴OA=OC=4,OB=OD=3,AC⊥BD,
在Rt△AOB中,AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵S菱形ABCD=$\frac{1}{2}$•AC•BD,
S菱形ABCD=DH•AB,
∴DH•5=$\frac{1}{2}$•6•8,
∴DH=$\frac{24}{5}$.
故答案为$\frac{24}{5}$.
点评 本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;菱形的面积等于对角线乘积的一半.

练习册系列答案
相关题目
2.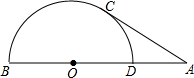 如图,点D为定线段AB上一动点,以BD为直径作半圆O,过A作半圆O的切线,切点为C,连CD,当(AC-AD)取最大值时,tan∠ACD=( )
如图,点D为定线段AB上一动点,以BD为直径作半圆O,过A作半圆O的切线,切点为C,连CD,当(AC-AD)取最大值时,tan∠ACD=( )
 如图,点D为定线段AB上一动点,以BD为直径作半圆O,过A作半圆O的切线,切点为C,连CD,当(AC-AD)取最大值时,tan∠ACD=( )
如图,点D为定线段AB上一动点,以BD为直径作半圆O,过A作半圆O的切线,切点为C,连CD,当(AC-AD)取最大值时,tan∠ACD=( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
6.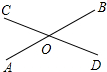 如图,直线AB与CD相交于点O,若∠AOC=$\frac{1}{3}$∠AOD,则∠BOD的度数为( )
如图,直线AB与CD相交于点O,若∠AOC=$\frac{1}{3}$∠AOD,则∠BOD的度数为( )
 如图,直线AB与CD相交于点O,若∠AOC=$\frac{1}{3}$∠AOD,则∠BOD的度数为( )
如图,直线AB与CD相交于点O,若∠AOC=$\frac{1}{3}$∠AOD,则∠BOD的度数为( )| A. | 30° | B. | 45° | C. | 60° | D. | 135° |
3. 如图,直线AB、CD相交于点O,∠AOD与∠BOC的和为264°,那么∠AOC的度数是( )
如图,直线AB、CD相交于点O,∠AOD与∠BOC的和为264°,那么∠AOC的度数是( )
 如图,直线AB、CD相交于点O,∠AOD与∠BOC的和为264°,那么∠AOC的度数是( )
如图,直线AB、CD相交于点O,∠AOD与∠BOC的和为264°,那么∠AOC的度数是( )| A. | 58° | B. | 132° | C. | 48° | D. | 46° |
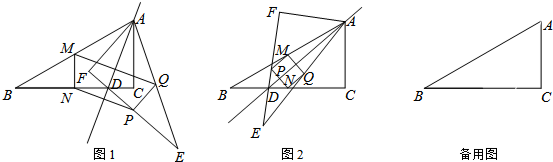
 如图,已知AB∥CD,∠1=∠2,求证:BE∥GF.
如图,已知AB∥CD,∠1=∠2,求证:BE∥GF.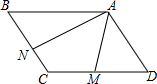 如图,在?ABCD中,点M,N分别是边CD、BC的中点,AM=2,AN=4,且∠MAN=60°,则AB的长是$\frac{4\sqrt{13}}{3}$.
如图,在?ABCD中,点M,N分别是边CD、BC的中点,AM=2,AN=4,且∠MAN=60°,则AB的长是$\frac{4\sqrt{13}}{3}$.