题目内容
15.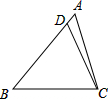 在△ABC中,D为AB边上一点,且∠BCD=∠A.已知BC=$2\sqrt{2}$,AB=3,则BD=$\frac{8}{3}$.
在△ABC中,D为AB边上一点,且∠BCD=∠A.已知BC=$2\sqrt{2}$,AB=3,则BD=$\frac{8}{3}$.
分析 证明△DCB≌△CAB,得$\frac{BD}{BC}$=$\frac{CB}{AB}$,由此即可解决问题.
解答 解:∵∠BCD=∠A,∠B=∠B,
∴△DCB~△CAB,
∴$\frac{BD}{BC}$=$\frac{CB}{AB}$,
∴$\frac{BD}{2\sqrt{2}}$=$\frac{2\sqrt{2}}{3}$,
∴BD=$\frac{8}{3}$.
故答案为$\frac{8}{3}$.
点评 本题考查相似三角形的判定和性质,解题的关键是熟练掌握相似三角形的判定方法,利用相似三角形的性质解决问题,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.下列尺规作图,能判断AD是△ABC边上的高是( )
| A. |  | B. |  | C. |  | D. |  |
3.某种油菜籽在相同条件下的发芽试验结果如下:
由此可以估计油菜籽发芽的概率约为0.95(精确到0.01),其依据是频率的稳定性.
| 每批粒数n | 100 | 300 | 400 | 600 | 1000 | 2020 | 3000 |
| 发芽的频数m | 96 | 283 | 344 | 552 | 948 | 1912 | 2848 |
| 发芽的频率 | 0.96 | 0.94 | 0.86 | 0.92 | 0.95 | 0.95 | 0.95 |
7.若点(-3,y1),(-2,y2),(2,y3)都在反比例函数y=$\frac{3}{x}$的图象上,则( )
| A. | y1>y2>y3 | B. | y2>y1>y3 | C. | y3>y1>y2 | D. | y1>y3>y2 |
5. 菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若EF=$\sqrt{2}$,BD=2,则菱形ABCD的面积为( )
菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若EF=$\sqrt{2}$,BD=2,则菱形ABCD的面积为( )
 菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若EF=$\sqrt{2}$,BD=2,则菱形ABCD的面积为( )
菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若EF=$\sqrt{2}$,BD=2,则菱形ABCD的面积为( )| A. | 2$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | 6$\sqrt{2}$ | D. | 8$\sqrt{2}$ |
 如图,正六边形ABCDEF内接于半径为3的圆O,则劣弧AB的长度为π.
如图,正六边形ABCDEF内接于半径为3的圆O,则劣弧AB的长度为π. 小明参加某超市的翻笑脸抽奖活动,如图,四张笑脸背后分别对应价值50,100,100,200(单位:元)的代金券
小明参加某超市的翻笑脸抽奖活动,如图,四张笑脸背后分别对应价值50,100,100,200(单位:元)的代金券