Question

3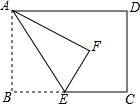．如图，在矩形ABCD中，点E为BC边上一点，连接AE，将△ABE沿AE折叠得到△AFE，且EF的延长线恰好经过点D，若BE=2，CE=3，则AE的长为（　　）

• A． 2$\sqrt{6}$
• B． 5
• C． 2$\sqrt{5}$
• D． 4

Answer 1

分析 先证明△ADF≌△DEC，从而得到DF=EC=3，然后再△DEC中由勾股定理求得DC=4，最后再△ABE中利用勾股定理即可求得AE的长．

解答 解：如图所示：连接FD．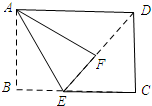

∵四边形ABCD为矩形，
∴AC=DC．∠B=90°．
由翻折的性质可知；AB=AF，∠AFE=∠B=90°，BE=BF=2．
∴AF=DC．
∵EF的延长线恰好经过点D，
∴E、F、D在一条直线上，
∴∠AFD=90°．
∵AD∥BC，
∴∠ADF=∠DEC．
在△ADF和△DEC中，$\left\{\begin{array}{l}{∠ADF=∠DEC}\\{AF=DC}\\{∠AFD=∠C}\end{array}\right.$，
∴△ADF≌△DEC．
∴DF=EC=3．
∴ED=2+3=5．
在Rt△DEC中，由勾股定理得：DC=$\sqrt{D{E}^{2}-E{C}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4．
∴AB=4．
在Rt△ABE中，由勾股定理得：AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$．
故选：C．

点评 本题主要考查的是翻折的性质、勾股定理、全等三角形的判定和性质，证得△ADF≌△DEC是解题的关键．