题目内容
12．已知梯形的两条对角线把中位线三等分，则梯形上底与下底的比为（ ）| A． | 1：2 | B． | 1：3 | C． | 2：3 | D． | 3：5 |
分析 设梯形的中位线为3x，根据梯形中位线定理和平行线等分线段定理得到EG是△ABD的中位线和GF是△CBD的中位线，即可得到答案．
解答 解：
设梯形的中位线为3x，
则EG=GH=HF=x，
∵EF是梯形的中位线，
∴EF∥AD∥BC，
∵E是AB的中点，
∴EG是△ABD的中位线，∴AD=2EG=2x，
∵F是CD的中点，
∴GF是△CBD的中位线，∴BC=2GF=4x，
∴AD：BC=1：2，
故选：A．
点评 本题考查的是梯形和三角形中位线定理，掌握梯形的中位线平行于两底且等于两底和的一半是解题的关键．
练习册系列答案
相关题目
如图，在矩形ABCD中，AB=6cm，BC=8cm，点P从A开始沿AB边向点B以1cm/s的速度移动，点Q从点B边开始沿BC边向点C以2cm/s的速度移动．
3．
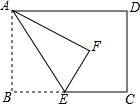如图，在矩形ABCD中，点E为BC边上一点，连接AE，将△ABE沿AE折叠得到△AFE，且EF的延长线恰好经过点D，若BE=2，CE=3，则AE的长为（ ）
如图，在矩形ABCD中，点E为BC边上一点，连接AE，将△ABE沿AE折叠得到△AFE，且EF的延长线恰好经过点D，若BE=2，CE=3，则AE的长为（ ）| A． | 2$\sqrt{6}$ | B． | 5 | C． | 2$\sqrt{5}$ | D． | 4 |
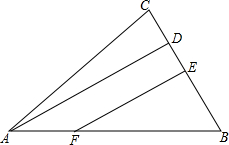已知：如图，AD⊥BC于D，E为BC中点，EF⊥BC交AB于F，AB=9cm，BC=6cm，DC=2cm，求AF的长．
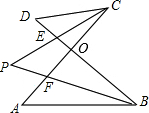如图，AC、BD相交于点O，BP、CP分别平分∠ABD、∠ACD，且相交于点P．
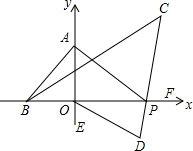如图，在平面直角坐标系中，∠ABO=2∠BAO，P为x轴正半轴一动点，BC平分∠ABP，PC平分∠APF，OD平分∠POE