如图.已知∠1+∠2=180°.∠3=∠B.试说明∠AED=∠ACB．题目和参考答案——青夏教育精英家教网—

题目内容

20．

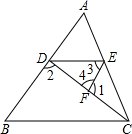如图，已知∠1+∠2=180°，∠3=∠B，试说明∠AED=∠ACB．

分析首先判断∠AED与∠ACB是一对同位角，然后根据已知条件推出DE∥BC，得出两角相等．

解答证明：∵∠1+∠4=180°（平角定义），∠1+∠2=180°（已知），
∴∠2=∠4，
∴EF∥AB（内错角相等，两直线平行），
∴∠3=∠ADE（两直线平行，内错角相等），
∵∠3=∠B（已知），
∴∠B=∠ADE（等量代换），
∴DE∥BC（同位角相等，两直线平行），
∴∠AED=∠ACB（两直线平行，同位角相等）．

点评本题主要考查了平行线的性质和判定，综合运用平行线的判定与性质定理是解答此题的关键．

练习册系列答案

11．如图，正方形ABCD在平面直角坐标系中，各顶点的坐标分别为A（-4，4），B（-4，0），C（0，0），D（0，4）．P、Q分别从点B、O出发，均以每秒1个单位的速度沿x轴向右运动，运动时间t（s）：作PE⊥PA，QE⊥x轴交于点E，直线AE交y轴于点F．
（1）求证：PA=PE；
（2）连接DE，求当t为何值时，线段DE的长最小？并求DE长的最小值；
（3）连接PF，设y=PO+OF+FP，求y关于t的函数关系式．

8．计算题：
（1）$\sqrt{2}$（$\sqrt{2}$+2）
（2）$\sqrt{36}$×$\sqrt{\frac{1}{9}}$-$\root{3}{27}$
（3）$\sqrt{\frac{25}{16}}$+$\root{3}{-8}$-（$\frac{1}{2}$）²
（4）|1-$\sqrt{2}$|+|$\sqrt{2}$-$\sqrt{3}$|+|2$\sqrt{3}$-3|

15．若关于x的方程$\frac{1}{x-1}$=$\frac{2}{x-a}$的解为正数，则a的取值范围是a＜2且a≠1．

5．下列判断不正确的是（　　）

	A．	四个角相等的四边形是矩形		B．	对角线垂直的四边形是菱形
	C．	对角线相等的平行四边形是矩形		D．	对角线垂直的平行四边形是菱形

12．

已知四边形ABCD的对角线AC、BD相交于点O，给出下列5个条件：①AB∥CD；②OA=OC；③AB=CD；④∠BAD=∠DCB；⑤AD∥BC，从以上5个条件中任选2个条件为一组，能判定四边形ABCD是平行四边形的有（　　）组．

9．若$\sqrt{2x-3}$是二次根式，则x应满足的条件是（　　）

10．一个长方形的面积是2a²-2b²，如果它的一条边长是a-b，则它的周长是6a+2b．

试题分类