题目内容
8.计算题:(1)$\sqrt{2}$($\sqrt{2}$+2)
(2)$\sqrt{36}$×$\sqrt{\frac{1}{9}}$-$\root{3}{27}$
(3)$\sqrt{\frac{25}{16}}$+$\root{3}{-8}$-($\frac{1}{2}$)2
(4)|1-$\sqrt{2}$|+|$\sqrt{2}$-$\sqrt{3}$|+|2$\sqrt{3}$-3|
分析 (1)原式利用二次根式乘法法则计算即可得到结果;
(2)原式利用二次根式乘法法则,以及立方根定义计算即可得到结果;
(3)原式利用算术平方根,立方根的定义,以及乘方的意义计算即可得到结果;
(4)原式利用绝对值的代数意义化简,计算即可得到结果.
解答 解:(1)原式=2+2$\sqrt{2}$;
(2)原式=6×$\frac{1}{3}$-3=2-3=-1;
(3)原式=$\frac{5}{4}$-2-$\frac{1}{4}$=-1;
(4)原式=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+2$\sqrt{3}$-3=3$\sqrt{3}$-4.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
18.弹簧挂上物体后会伸长,已知一弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系如表:
(1)上表反映的变量之间的关系中自变量是物体的质量,因变量是弹簧的长度.
(2)当所挂物体是3kg时,弹簧的长度是13.5cm,不挂重物是12cm.
(3)直接写出y与x的关系式,并求出当弹簧长度为17cm时所挂物体质量.
| 物体的质量x(kg) | 0 | 1 | 2 | 3 | 4 | 5 |
| 弹簧的长度y(cm) | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 |
(2)当所挂物体是3kg时,弹簧的长度是13.5cm,不挂重物是12cm.
(3)直接写出y与x的关系式,并求出当弹簧长度为17cm时所挂物体质量.
13.下列命题中,真命题是( )
| A. | 两条对角线垂直且相等的四边形是正方形 | |
| B. | 两条对角线互相垂直的四边形是菱形 | |
| C. | 两条对角线互相平分且相等的四边形是矩形 | |
| D. | 一组对边平行,另一组对边相等的四边形是平行四边形 |
 如图,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠ACB.
如图,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠ACB.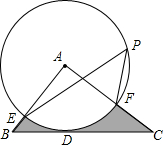 如图,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F,点P是⊙A上的一点,且∠EPF=45°,则图中阴影部分的面积为( )
如图,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F,点P是⊙A上的一点,且∠EPF=45°,则图中阴影部分的面积为( )