题目内容
15.若关于x的方程$\frac{1}{x-1}$=$\frac{2}{x-a}$的解为正数,则a的取值范围是a<2且a≠1.分析 根据解分式方程的一般步骤,可得分式方程的解,根据解为正数,可得不等式,根据解不等式,可得答案.
解答 解:分式方程$\frac{1}{x-1}=\frac{2}{x-a}$的解为:x=2-a,
∵分式方程的解为正数,
∴2-a>0,
解得:a<2.
∵x-1≠0,
∴2-a-1≠1
∴a≠1,
故答案为:a<2且a≠1.
点评 本题考查了分式方程的解,解决本题的关键是解分式方程.注意分式方程中分母不为0.

练习册系列答案
相关题目
6.如图①,在四边形ABCD中,AD∥BC,∠A=60°,动点P从A点出发,以1cm/s的速度沿着A→B→C→D的方向向点D移动,已知△PAD的面积S(单位:cm2)与点P移动的时间t(单位:s)的函数如图②所示,则点P从开始移动到停止共用时( )
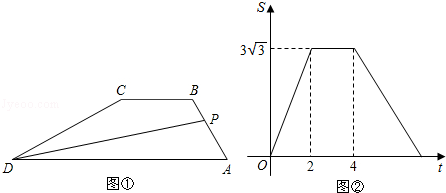

| A. | 8秒 | B. | (4+$2\sqrt{3}$)秒 | C. | (4+3$\sqrt{3}$)秒 | D. | (4+$\sqrt{3}$)秒 |
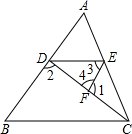 如图,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠ACB.
如图,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠ACB. 如图,已知点C为AB上一点,AC=12cm,CB=$\frac{1}{2}$AC,D、E分别为AC、AB的中点,求DE的长.
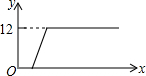
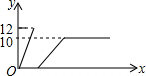
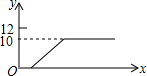
如图,已知点C为AB上一点,AC=12cm,CB=$\frac{1}{2}$AC,D、E分别为AC、AB的中点,求DE的长.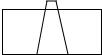 如图,将一个高度为12cm的锥形瓶放入一个空玻璃槽中,并向锥形瓶中匀速注水,若水槽的高度为10cm,则水槽中的水面高度y(cm)随注水时间x(s)的变化图象大致是( )
如图,将一个高度为12cm的锥形瓶放入一个空玻璃槽中,并向锥形瓶中匀速注水,若水槽的高度为10cm,则水槽中的水面高度y(cm)随注水时间x(s)的变化图象大致是( )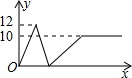
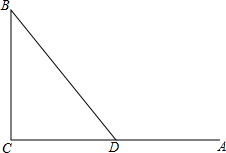 如图,A、B、C三个地点(图中的线段均是道路),AC⊥BC,甲、乙两人同时从A地出发,已知甲的速度比乙的速度快$\frac{1}{4}$,如果经C地到达B地,且使乙比甲早到B地,这是一个不可能的情况,但在距A地200米的D处有一条路可直通B地(即图中BD).
如图,A、B、C三个地点(图中的线段均是道路),AC⊥BC,甲、乙两人同时从A地出发,已知甲的速度比乙的速度快$\frac{1}{4}$,如果经C地到达B地,且使乙比甲早到B地,这是一个不可能的情况,但在距A地200米的D处有一条路可直通B地(即图中BD).