题目内容
13.若|m-2|+($\frac{n}{3}$-1)2=0,则单项式3x2ym+n-1和x${\;}^{{n}^{2}-2m}$y4是同类项吗?如果是,请把它们进行加法运算;如果不是同类项,请从下列代数式中找出同类项进行加法运算:-2x2y4,-5x6y4.分析 先根据题意求出m与n的值,然后把m与n的值代入3x2ym+n-1和x${\;}^{{n}^{2}-2m}$y4进行化简,最后根据合并同类项的法则求出答案即可.
解答 解:∵|m-2|+($\frac{n}{3}$-1)2=0,
∴m-2=0,$\frac{n}{3}$-1=0,
∴m=2 n=3
∴m+n-1=4,n2-2m=5,
∴单项式为:3x2y4与x5y4,不是同类项,
∴3x2y4+(-2x2y4)=x2y4
点评 本题考查同类项的概念,解题的关键是求出m与n的值,然后化简原单项式,本题属于基础题型.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
8.我们把大于1的正整数m的三次幂按一定的规则“分裂”成若干个连续奇数的和,如23=3+5,33=7+9+11,43=13+15+17+19,…若m3按此规则“分裂”后,最后一个奇数是341,则m的值为( )
| A. | 17 | B. | 18 | C. | 19 | D. | 20 |
18.下列事件:①随意翻到一本书的某页,这页的页码是奇数;②测得某天的最高气温是100℃;③掷一次骰子,向上一面的数字是2;④度量四边形的内角和,结果是360°.其中随机事件有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
5.如果$\sqrt{m+n}$=3,那么(m+n)2等于( )
| A. | 3 | B. | 9 | C. | 27 | D. | 81 |
 如图,AB是⊙O的直径,AC是⊙O的弦,过点C的切线交AB的延长线于点D,且∠A=∠D.
如图,AB是⊙O的直径,AC是⊙O的弦,过点C的切线交AB的延长线于点D,且∠A=∠D. 如图是一个三角形数阵:根据该数阵的规律,猜想第九行所有数的和是729.
如图是一个三角形数阵:根据该数阵的规律,猜想第九行所有数的和是729.



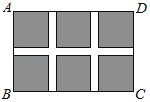 如图,某小区规划在一个长30m,宽20m的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草,设通道的宽为xm.
如图,某小区规划在一个长30m,宽20m的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草,设通道的宽为xm.