题目内容
8.我们把大于1的正整数m的三次幂按一定的规则“分裂”成若干个连续奇数的和,如23=3+5,33=7+9+11,43=13+15+17+19,…若m3按此规则“分裂”后,最后一个奇数是341,则m的值为( )| A. | 17 | B. | 18 | C. | 19 | D. | 20 |
分析 观察可知,分裂成的奇数的个数与底数相同,然后求出到m3的所有奇数的个数的表达式,再求出奇数341的是从3开始的第170个数,然后确定出170所在的范围即可得解.
解答 解:∵底数是2的分裂成2个奇数,底数为3的分裂成3个奇数,底数为4的分裂成4个奇数,
∴m3有m个奇数,
所以,到m3的奇数的个数为:2+3+4+…+m=$\frac{(m+2)(m-1)}{2}$,
∵2n+1=341,n=170,
∴奇数341是从3开始的第170个奇数,
∵$\frac{(17+2)(17-1)}{2}$=152,$\frac{(18+2)(18-1)}{2}$=170,
∴第170个奇数是底数为18的数的立方分裂的奇数的最后一个,
即m=18,
故选:B.
点评 此题考查数字的变化类和有理数的混合运算,重点考查分析问题和解决问题以及计算方面的能力,确定每一个“拆分数”中第一个数构成的数列的规律是关键.

练习册系列答案
相关题目
18.已知二次函数y=x2+bx+c的图象经过点(-1,-2),则bc有( )
| A. | 最小值-$\frac{1}{4}$ | B. | 最小值-$\frac{9}{4}$ | C. | 最大值$\frac{1}{4}$ | D. | 最大值$\frac{9}{4}$ |
19.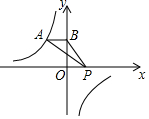 如图,A为反比例函数y=$\frac{k}{x}$图象上的一点,AB⊥y轴于B,点P在x轴上,S△ABP=2,则这个反比例函数的表达式为( )
如图,A为反比例函数y=$\frac{k}{x}$图象上的一点,AB⊥y轴于B,点P在x轴上,S△ABP=2,则这个反比例函数的表达式为( )
 如图,A为反比例函数y=$\frac{k}{x}$图象上的一点,AB⊥y轴于B,点P在x轴上,S△ABP=2,则这个反比例函数的表达式为( )
如图,A为反比例函数y=$\frac{k}{x}$图象上的一点,AB⊥y轴于B,点P在x轴上,S△ABP=2,则这个反比例函数的表达式为( )| A. | y=$\frac{2}{x}$ | B. | y=-$\frac{2}{x}$ | C. | y=$\frac{4}{x}$ | D. | y=-$\frac{4}{x}$ |
3.下列语句中,说法错误的是( )
| A. | 点(0,0)是坐标原点 | |
| B. | 对于坐标平面内的任一点,都有唯一的一对有序实数与它对应 | |
| C. | 点A(a,-b )在第二象限,则点B(-a,b)在第四象限 | |
| D. | 若点P的坐标为(a,b),且a•b=0,则点P一定在坐标原点 |
20.若a,b是实数,且a2=$\sqrt{b-1}+\sqrt{1-b}+4$,则a+b的值是( )
| A. | 3或-3 | B. | 3或-1 | C. | -3或-1 | D. | 3或1 |
18.下列各组长度的线段能构成三角形的是( )
| A. | 1cm 2cm 3cm | B. | 2cm 3cm 4cm | ||
| C. | 1cm 2cm 3.5cm | D. | 2cm 2cm 4cm |
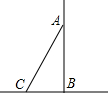 如图,将长为6米的梯子AC斜靠在墙上,BC长为2米,求梯子上端A到墙的底端B的距离AB.
如图,将长为6米的梯子AC斜靠在墙上,BC长为2米,求梯子上端A到墙的底端B的距离AB.