题目内容
4．二次函数y=-x2+6x+2的最大值是11．分析 先利用配方法把一般式配成顶点式，然后根据二次函数的性质求解．
解答 解：原式=-x2+6x+2
=-（x-3）2+11，
因为抛物线开口向下，
所以当x=1时，y有最大值11．
故答案为11．
点评 本题考查了二次函数的最值：当a＞0时，抛物线在对称轴左侧，y随x的增大而减少；在对称轴右侧，y随x的增大而增大，因为图象有最低点，所以函数有最小值，．确定一个二次函数的最值，首先看自变量的取值范围，当自变量取全体实数时，其最值为抛物线顶点坐标的纵坐标；当自变量取某个范围时，要分别求出顶点和函数端点处的函数值，比较这些函数值，从而获得最值．
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
名师点睛字词句段篇系列答案
相关题目
下面的框图表示解方程3x-7（x-1）=3-2（x+3）的流程，其中A代表的步骤是移项，步骤A对方程进行变形的依据是等式的基本性质1．
19．
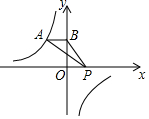如图，A为反比例函数y=$\frac{k}{x}$图象上的一点，AB⊥y轴于B，点P在x轴上，S△ABP=2，则这个反比例函数的表达式为（ ）
如图，A为反比例函数y=$\frac{k}{x}$图象上的一点，AB⊥y轴于B，点P在x轴上，S△ABP=2，则这个反比例函数的表达式为（ ）| A． | y=$\frac{2}{x}$ | B． | y=-$\frac{2}{x}$ | C． | y=$\frac{4}{x}$ | D． | y=-$\frac{4}{x}$ |
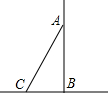如图，将长为6米的梯子AC斜靠在墙上，BC长为2米，求梯子上端A到墙的底端B的距离AB．