题目内容
5.计算:(1)(a-2b)2-a(a-4b)
(2)($\frac{8-4x}{x+2}$-2+x)÷$\frac{{x}^{2}-2x}{x+2}$.
分析 (1)根据完全平方公式、单项式乘多项式可以解答本题;
(2)根据分式的减法和除法可以解答本题.
解答 解:(1)(a-2b)2-a(a-4b)
=a2-4ab+4b2-a2+4ab
=4b2;
(2)($\frac{8-4x}{x+2}$-2+x)÷$\frac{{x}^{2}-2x}{x+2}$
=$\frac{8-4x-(2-x)(x+2)}{x+2}•\frac{x+2}{x(x-2)}$
=$\frac{8-4x-4+{x}^{2}}{x(x-2)}$
=$\frac{(x-2)^{2}}{x(x-2)}$
=$\frac{x-2}{x}$.
点评 本题考查分式的混合运算、单项式乘多项式、完全平方公式,解答本题的关键是明确它们各自的计算方法.

练习册系列答案
相关题目
10.下列计算正确的是( )
| A. | 2m+3m=5m2 | B. | 2m•3m2=6m2 | C. | (m3)2=m6 | D. | m6÷m2=m3 |


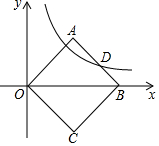 如图,已知正方形OABC的一个顶点在原点,且对角线OB在x轴的正半轴上,反比例函数y=$\frac{k}{x}$在第一象限内的图象与AB边交于点D,若OA2-AD2=8,求反比例函数的解析式.
如图,已知正方形OABC的一个顶点在原点,且对角线OB在x轴的正半轴上,反比例函数y=$\frac{k}{x}$在第一象限内的图象与AB边交于点D,若OA2-AD2=8,求反比例函数的解析式.