题目内容
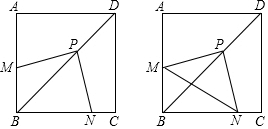
20.问题背景:如图(1)在四边形ABCD中,∠ACB=∠ADB=90°,AD=BD,探究线段AC、BC、CD之间的数量关系.小吴探究此问题的思路是:将△BCD绕点D逆时针旋转90°到△AED处,点B、C分别落在点A、E处(如图(2)),易证点C、A、E在同一条直线上,并且△CDE是等腰直角三角形,所以CE=$\sqrt{2}$CD,从而得出结论:AC+BC=$\sqrt{2}$CD.简单应用:
(1)在图(1)中,若AC=$\sqrt{2}$,BC=2$\sqrt{2}$,则CD=3;
(2)如图(3)AB是⊙O的直径,点C、D在⊙O上,AD=BD,若AB=13,BC=12,求CD的长.

分析 (1)代入结论:AC+BC=$\sqrt{2}$CD,直接计算即可;
(2)如图3,作辅助线,根据直径所对的圆周角是直角得:∠ADB=∠ACB=90°,由弧相等可知所对的弦相等,得到满足图1的条件,所以AC+BC=$\sqrt{2}$CD,代入可得CD的长;
解答 解:(1)由题意知:AC+BC=$\sqrt{2}$CD,
∴$\sqrt{2}$+2 $\sqrt{2}$=$\sqrt{2}$CD,
∴CD=3;
故答案为:3;
(2)如图3,连接AC、BD、AD,
∵AB是⊙O的直径,
∴∠ADB=∠ACB=90°,
∵$\widehat{AD}$=$\widehat{BD}$,
∴AD=BD,
∵AB=13,BC=12,
∴由勾股定理得:AC=5,
由图1得:AC+BC=$\sqrt{2}$CD,
5+12=$\sqrt{2}$CD,
∴CD=$\frac{17}{2}$$\sqrt{2}$;
点评 本题是圆和四边形的综合题,考查了圆周角定理、弦和弧的关系、勾股定理、旋转的性质、等腰直角三角形的性质等知识,解题的关键是学会应用结论解决问题,属于中考常考题型.

练习册系列答案
相关题目
11.某商品的进价为每件20元.当售价为每件30元时,每天可卖出100件,现需降价处理,且经市场调查:每降价1元,每天可多卖出10件.现在要使每天利润为750元,每件商品应降价( )元.
| A. | 2 | B. | 2.5 | C. | 3 | D. | 5 |
8.一组数据2,5,6,x,4的平均数是4,这组数据的方差是( )
| A. | 10 | B. | 2 | C. | $\sqrt{10}$ | D. | $\sqrt{2}$ |
12.当a=1,b=-2时,代数式2a2-ab的值是( )
| A. | -4 | B. | 0 | C. | 4 | D. | 7 |
9.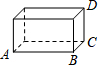 如图:长方体的长AB=4厘米、宽BC=2厘米、高CD=3厘米.一只蚂蚁想从A点沿表面爬到D点,则最短距离是( )
如图:长方体的长AB=4厘米、宽BC=2厘米、高CD=3厘米.一只蚂蚁想从A点沿表面爬到D点,则最短距离是( )
 如图:长方体的长AB=4厘米、宽BC=2厘米、高CD=3厘米.一只蚂蚁想从A点沿表面爬到D点,则最短距离是( )
如图:长方体的长AB=4厘米、宽BC=2厘米、高CD=3厘米.一只蚂蚁想从A点沿表面爬到D点,则最短距离是( )| A. | 3$\sqrt{5}$ | B. | $\sqrt{41}$ | C. | $\sqrt{29}$ | D. | 5 |