题目内容
15.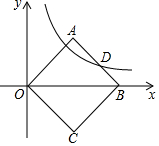 如图,已知正方形OABC的一个顶点在原点,且对角线OB在x轴的正半轴上,反比例函数y=$\frac{k}{x}$在第一象限内的图象与AB边交于点D,若OA2-AD2=8,求反比例函数的解析式.
如图,已知正方形OABC的一个顶点在原点,且对角线OB在x轴的正半轴上,反比例函数y=$\frac{k}{x}$在第一象限内的图象与AB边交于点D,若OA2-AD2=8,求反比例函数的解析式.
分析 先过点D作DE⊥OB于E,连接OD,设D(a,b),则DE=b,OE=a,根据∠DBE=45°,求得OA=$\frac{\sqrt{2}}{2}$(a+b),AD=$\frac{\sqrt{2}}{2}$(a-b),代入OA2-AD2=8,即可得出ab的值,进而得到反比例函数的解析式.
解答 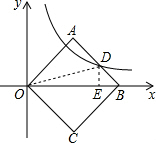 解:如图,过点D作DE⊥OB于E,连接OD,
解:如图,过点D作DE⊥OB于E,连接OD,
设D(a,b),则DE=b,OE=a,
∵四边形OABC是正方形,
∴∠DBE=45°,
∴BE=DE=b,OB=a+b,BD=$\sqrt{2}$b,
∴等腰Rt△AOB中,OA=AB=$\frac{OB}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$(a+b),
AD=AB-BD=$\frac{\sqrt{2}}{2}$(a+b)-$\sqrt{2}$b=$\frac{\sqrt{2}}{2}$(a-b),
∵OA2-AD2=8,
∴[$\frac{\sqrt{2}}{2}$(a+b)]2-[$\frac{\sqrt{2}}{2}$(a-b)]2=8,
解得ab=4,
∵反比例函数y=$\frac{k}{x}$在第一象限内的图象经过点D,
∴k=ab=4,
∴反比例函数的解析式为y=$\frac{4}{x}$.
点评 本题主要考查了正方形的性质以及待定系数法求反比例函数解析式,解决问题的关键是运用数形结合思想,利用点D的坐标求得反比例函数系数k的值.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目
11.下列结论正确的是( )
| A. | 若a2=b2,则a=b | B. | 若a>b,则a2>b2 | ||
| C. | 若a,b不全为零,则a2+b2>0 | D. | 若a≠b,则a2≠b2 |
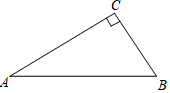 折叠如图所示的直角三角形纸片ABC,使点C落在AB上的点E处,折痕为AD(点D在BC边上),用直尺和圆规画出折痕AD.(保留作图痕迹,不写作法).
折叠如图所示的直角三角形纸片ABC,使点C落在AB上的点E处,折痕为AD(点D在BC边上),用直尺和圆规画出折痕AD.(保留作图痕迹,不写作法).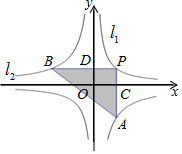 如图,两个反比例函数$y=\frac{k}{x}$和y=-$\frac{2}{x}$的图象分别是l1和l2,E(2,$\frac{1}{2}$)是l1上的一点.
如图,两个反比例函数$y=\frac{k}{x}$和y=-$\frac{2}{x}$的图象分别是l1和l2,E(2,$\frac{1}{2}$)是l1上的一点. 如图,两条直线表示函数y1=k1x与y2=k2x+b的图象,根据图象回答:
如图,两条直线表示函数y1=k1x与y2=k2x+b的图象,根据图象回答: