题目内容
如图，ABCD为正方形，E、F分别为AD、BC的中点，M为DC边上一动点，沿BM折叠△BCM，点C落在正方形内的点P处，BM与EF相交于点Q．（1）如图1，
| BQ |
| BM |
（2）如图2，当点P恰好落在EF上时，
| CM |
| CD |
考点：翻折变换（折叠问题）,正方形的性质
专题：
分析：（1）根据三角形中位线定理即可得到
的值；
（2）在Rt△BPF中，根据三角函数可得∠PBF=60°，再根据折叠的性质可得∠MBF=30°，根据三角函数和正方形的性质可得
的值．
| BQ |
| BM |
（2）在Rt△BPF中，根据三角函数可得∠PBF=60°，再根据折叠的性质可得∠MBF=30°，根据三角函数和正方形的性质可得
| CM |
| CD |
解答：解：（1）∵E、F分别为AD、BC的中点，
∴FQ是△BCM的中位线，
∴
=
；
（2）在Rt△BPF中，cos∠PBF=
=
，
∴∠PBF=60°，
由折叠的性质可得∠MBF=30°，
∴
=
=tan∠MBF=
．
故答案为：
；
．
∴FQ是△BCM的中位线，
∴
| BQ |
| BM |
| 1 |
| 2 |
（2）在Rt△BPF中，cos∠PBF=
| BF |
| BP |
| 1 |
| 2 |
∴∠PBF=60°，
由折叠的性质可得∠MBF=30°，
∴
| CM |
| CD |
| CM |
| BC |
| ||
| 3 |
故答案为：
| 1 |
| 2 |
| ||
| 3 |
点评：考查了翻折变换（折叠问题），正方形的性质，三角形中位线定理和三角函数的知识，综合性较强，难度中等．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
如图，E是矩形ABCD的边BC上的一点，EF⊥AE，EF分别交AC，CD于点M，F，BG⊥AC，垂足为G，BG交AE于点H．
如图，⊙O是以原点为圆心，
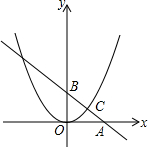如图，直线y=kx+b交坐标轴于A、B两点，交抛物线y=ax2于点C（4，3），且C是线段AB的中点，抛物线上另有位于第一象限内的一点P，过P的直线y=k′x+b′交坐标轴于D、E两点，且P恰好是线段DE的中点，若△AOB∽△DOE，则P点的坐标是
如图，边长为1的正方形ABCD绕点A逆时针旋转45°到正方形AB′C′D′，图中重合部分的面积为
如图，在Rt△ABC中，∠B=90°，sin∠BAC=
阅读材料：