题目内容
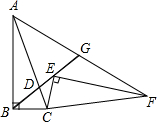 如图,在Rt△ABC中,∠B=90°,sin∠BAC=
如图,在Rt△ABC中,∠B=90°,sin∠BAC=| 1 |
| 3 |
A、
| ||||
B、3
| ||||
C、3
| ||||
D、
|
考点:旋转的性质
专题:
分析:根据旋转的性质可得BC=CE,AC=CF,∠BCE=∠ACF,再根据等腰三角形两底角相等求出∠CBD=∠CAF,从而得到△BCD和△AGD相似,根据相似三角形对应边成比例求出AD=AG,过点B作BH⊥CD于H,根据等腰三角形三线合一的性质可得CD=2CH,再解直角三角形求出CH,AC,然后根据AD=AC-CD代入数据进行计算即可得解.
解答:解:作BH⊥DC于H点
∵△ABC以点C为旋转中心顺时针旋转得到△FEC,
∴BC=CE,AC=CF,∠BCE=∠ACF(为旋转角),
∵∠CBD=
(180°-∠BCE),∠CAF=
(180°-∠ACF),
∴∠CBD=∠CAF,
又∵∠BDC=∠ADG,
∴△BCD∽△AGD,
∴
=
,
∵BC=BD,
∴AG=AD,
则CD=2CH,
∵sin∠BAC=
,BC=2,
∴
=
=
,
即
=
=
,
解得CH=
,AC=6,
∴CD=2×
=
,
AD=AC-CD=6-
=
,
∴AG=AD=
,
故选:A.

∵△ABC以点C为旋转中心顺时针旋转得到△FEC,
∴BC=CE,AC=CF,∠BCE=∠ACF(为旋转角),
∵∠CBD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠CBD=∠CAF,
又∵∠BDC=∠ADG,
∴△BCD∽△AGD,
∴
| BC |
| BD |
| AG |
| AD |
∵BC=BD,
∴AG=AD,
则CD=2CH,
∵sin∠BAC=
| 1 |
| 3 |
∴
| CH |
| BC |
| BC |
| AC |
| 1 |
| 3 |
即
| CH |
| 2 |
| 2 |
| AC |
| 1 |
| 3 |
解得CH=
| 2 |
| 3 |
∴CD=2×
| 2 |
| 3 |
| 4 |
| 3 |
AD=AC-CD=6-
| 4 |
| 3 |
| 14 |
| 3 |
∴AG=AD=
| 14 |
| 3 |
故选:A.
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了全等三角形的判定与性质和勾股定理的逆定理.

练习册系列答案
相关题目
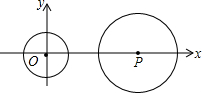 如图,平面直角坐标系中,⊙O半径长为1,点P(a,0),⊙P的半径长为2,把⊙P向左平移,与⊙P与⊙O相切时,a的值为( )
如图,平面直角坐标系中,⊙O半径长为1,点P(a,0),⊙P的半径长为2,把⊙P向左平移,与⊙P与⊙O相切时,a的值为( )| A、3 | B、1 | C、1,3 | D、±1,3 |
 如图,点O在边长为8的正方形ABCD的AD边上运动(4<C)A<8),以O为圆心,OA长为半径作圆,交CD于点E,连接OE、AE,过点E作直线EF交BC于点F,且∠CEF=2∠DAE.
如图,点O在边长为8的正方形ABCD的AD边上运动(4<C)A<8),以O为圆心,OA长为半径作圆,交CD于点E,连接OE、AE,过点E作直线EF交BC于点F,且∠CEF=2∠DAE. 如图,ABCD为正方形,E、F分别为AD、BC的中点,M为DC边上一动点,沿BM折叠△BCM,点C落在正方形内的点P处,BM与EF相交于点Q.
如图,ABCD为正方形,E、F分别为AD、BC的中点,M为DC边上一动点,沿BM折叠△BCM,点C落在正方形内的点P处,BM与EF相交于点Q. 如图,在菱形ABCD中,AB=BD,点E、F分别在AB、AD上,且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.下列结论:
如图,在菱形ABCD中,AB=BD,点E、F分别在AB、AD上,且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.下列结论: 如图,以矩形ABCD的顶点C为圆心作⊙C,⊙C分别交AB、CD于P、Q两点,当CB=2,CQ=4,CD=7时,阴影部分的面积为
如图,以矩形ABCD的顶点C为圆心作⊙C,⊙C分别交AB、CD于P、Q两点,当CB=2,CQ=4,CD=7时,阴影部分的面积为 Ⅰ.解不等式组5-x<2x-1≤9,并把解集在数轴上表示出来.
Ⅰ.解不等式组5-x<2x-1≤9,并把解集在数轴上表示出来.