题目内容
 阅读材料:
阅读材料:例:说明代数式
| x2+1 |
| (x-3)2+4 |
解:
| x2+1 |
| (x-3)2+4 |
| (x-0)2+12 |
| (x-3)2+22 |
| (x-0)2+12 |
| (x-3)2+22 |
设点A关于x轴的对称点为A′,则PA=PA′,因此,求PA+PB的最小值,只需求PA′+PB的最小值,而点A′、B间的直线段距离最短,所以PA′+PB的最小值为线段A′B的长度.为此,构造直角三角形A′CB,因为A′C=3,CB=3,所以A′B=3
| 2 |
| 2 |
根据以上阅读材料,解答下列问题:
(1)代数式
| (x-1)2+1 |
| (x-2)2+9 |
(2)求代数式
| x2+49 |
| x2-12x+37 |
考点:轴对称-最短路线问题,坐标与图形性质
专题:
分析:(1)根据阅读材料提供的方法写出点B的坐标即可;
(2)根据代数式的几何意义写出三点坐标,然后列式计算即可得解.
(2)根据代数式的几何意义写出三点坐标,然后列式计算即可得解.
解答:解:(1)点B坐标为(2,3);
故答案为:(2,3);
(2)∵
=
,
∴代数式
+
表示点(x,0)到点(0,7)和(6,1)的距离之和,
最小值为
=10.
故答案为:(2,3);
(2)∵
| x2-12x+37 |
| (x-6)2+1 |
∴代数式
| x2+49 |
| x2-12x+37 |
最小值为
| 62+(7+1)2 |
点评:本题考查了利用轴对称确定最短路线问题,坐标与图形性质,读懂题目信息理解代数式的几何意义以及最小值的求解方法是解题的关键.

练习册系列答案
相关题目
 如图,ABCD为正方形,E、F分别为AD、BC的中点,M为DC边上一动点,沿BM折叠△BCM,点C落在正方形内的点P处,BM与EF相交于点Q.
如图,ABCD为正方形,E、F分别为AD、BC的中点,M为DC边上一动点,沿BM折叠△BCM,点C落在正方形内的点P处,BM与EF相交于点Q.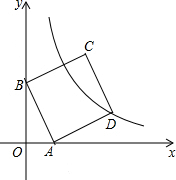 如图,在平面直角坐标系中,直线y=-3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限内作正方形ABCD,点D在反比例函数y=
如图,在平面直角坐标系中,直线y=-3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限内作正方形ABCD,点D在反比例函数y=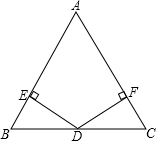 如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E、F.
如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E、F. Ⅰ.解不等式组5-x<2x-1≤9,并把解集在数轴上表示出来.
Ⅰ.解不等式组5-x<2x-1≤9,并把解集在数轴上表示出来.