题目内容
3．关于x的一元二次方程x2-px-p=0有两实数根x1、x2，若x${\;}_{1}^{2}$+x${\;}_{2}^{2}$=3，则p的值是1．分析 根据根与系数的关系得到x1+x2=p，x1•x2=-p，再变形x12+x22得到（x1+x2）2-2x1•x2，然后代入计算即可．
解答 解：∵关于x的一元二次方程x2-px-p=0有两实数根x1、x2，
∴x1+x2=p，x1•x2=-p，
∵x12+x22=（x1+x2）2-2x1•x2=p2+2p=3，
解得：p1=1，p2=-3，
∵p=-3时原方程无实数根，
∴p=1．
故答案为：1．
点评 本题考查了一元二次方程ax2+bx+c=0（a≠0）的根与系数的关系：若方程的两根为x1，x2，则x1+x2=-$\frac{b}{a}$，x1•x2=$\frac{c}{a}$．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
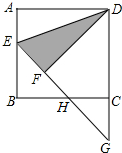如图，点E是正方形ABCD的边AB上一点，且∠ADE=22.5°，将△ADE沿DE翻折得到△FDE，延长EF交BC于点H，交DC的延长线于点G，则图中所有的等腰三角形是△EBH、△GHC、△EDG（将符合条件的所有三角形全部列举出来）．
如图，⊙O的直径CD⊥AB，∠AOC=60°，则∠CDB=30°．