题目内容
19.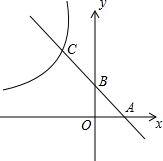 如图,直线y=-2x+1分别交x轴,y轴于点A,B,交反比例函数y=$\frac{k}{x}$的图象于点C,CB:BA=2:1.
如图,直线y=-2x+1分别交x轴,y轴于点A,B,交反比例函数y=$\frac{k}{x}$的图象于点C,CB:BA=2:1.(1)求反比例函数y=$\frac{k}{x}$的解析式;
(2)若点P在y轴上且以点B,C,P为顶点的三角形与△AOB相似,直接写出点P的坐标.
分析 (1)由直线的解析式求得A、B的坐标,进而根据CB:BA=2:1求得C的纵坐标,将C坐标代入直线y=-2x+1中求出横坐标,代入反比例函数y=$\frac{k}{x}$,确定出反比例解析式;
(2)分两种情况分别讨论即可求得.
解答 解:(1)∵直线y=-2x+1分别交x轴,y轴于点A,B,
∴A($\frac{1}{2}$,0),B(0,1),
∵CB:BA=2:1,
∴$\frac{AC}{BA}$=$\frac{3}{1}$,
作CD⊥x轴于D,则CD∥OB,
∴△ACD∽△ABO,
∴$\frac{CD}{OB}$=$\frac{AC}{BA}$,
∴$\frac{CD}{1}$=$\frac{3}{1}$,
∴CD=3,
把y=3代入y=-2x+1,解得x=-1,
∴C(-1,3),
代入y=$\frac{k}{x}$得,3=$\frac{k}{-1}$,
∴k=-3,
∴反比例函数y=$\frac{k}{x}$的解析式为y=-$\frac{3}{x}$;
(2)当△CPB∽△AOB时,
则$\frac{BP}{OB}$=$\frac{CP}{OA}$,即$\frac{BP}{1}$=$\frac{1}{\frac{1}{2}}$,
∴BP=2,
∴OP=OB+BP=1+2=3,
∴P(0,3);
当△PCB∽△AOB时,
则$\frac{PB}{BA}$=$\frac{BC}{OB}$,
∵OA=$\frac{1}{2}$,OB=1,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\frac{\sqrt{5}}{2}$,
∵CB:BA=2:1,
∴CB=$\sqrt{5}$,
∴$\frac{PB}{\frac{\sqrt{5}}{2}}$=$\frac{\sqrt{5}}{1}$,
∴PB=$\frac{5}{2}$,
∴OP=PB+0B=$\frac{5}{2}$+1=$\frac{7}{2}$,
∴P(0,$\frac{7}{2}$);
故P的坐标为(0,3)或(0,$\frac{7}{2}$).
点评 此题考查了一次函数与反比例函数的交点问题,涉及的知识有:坐标与图形性质,待定系数法确定函数解析式,一次函数与坐标轴的交点,三角形相似的性质,熟练掌握待定系数法是解本题的关键.

 习题精选系列答案
习题精选系列答案| A. | 相等 | B. | 互为相反数 | ||
| C. | 相等或互为相反数 | D. | 无法判断 |
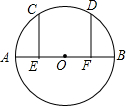 如图,AB是⊙O的直径,点E、F分别是OA、OB的中点,且EC⊥AB,FD⊥AB,EC、FD交⊙O于C、D两点,求证:$\widehat{AC}$=$\widehat{BD}$.
如图,AB是⊙O的直径,点E、F分别是OA、OB的中点,且EC⊥AB,FD⊥AB,EC、FD交⊙O于C、D两点,求证:$\widehat{AC}$=$\widehat{BD}$.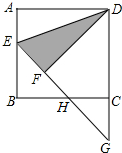 如图,点E是正方形ABCD的边AB上一点,且∠ADE=22.5°,将△ADE沿DE翻折得到△FDE,延长EF交BC于点H,交DC的延长线于点G,则图中所有的等腰三角形是△EBH、△GHC、△EDG(将符合条件的所有三角形全部列举出来).
如图,点E是正方形ABCD的边AB上一点,且∠ADE=22.5°,将△ADE沿DE翻折得到△FDE,延长EF交BC于点H,交DC的延长线于点G,则图中所有的等腰三角形是△EBH、△GHC、△EDG(将符合条件的所有三角形全部列举出来). 如图,⊙O的直径CD⊥AB,∠AOC=60°,则∠CDB=30°.
如图,⊙O的直径CD⊥AB,∠AOC=60°,则∠CDB=30°.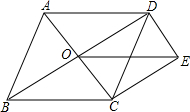 如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE.
如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE.