题目内容
在平面直角坐标系xOy中,A点坐标为(0,4),C点坐标为(10,0).若点P在直线y=kx+4上移动时,只存在一个点P使∠OPC=90°,则k的值是 .
考点:一次函数综合题
专题:
分析:设P的横坐标是x,则纵坐标是kx+4,点P在直线y=kx+4上移动时,只存在一个点P使∠OPC=90°,则P一定在以OC为圆心,以OC为直径的圆上,圆心坐标是(5,0),半径是5,根据P到OC的中点的距离等于半径5,即可列方程,且所列方程必须只有一个解,利用一元二次方程,根的判别式即可求解.
解答:解:设P的横坐标是x,则纵坐标是kx+4,
点P在直线y=kx+4上移动时,只存在一个点P使∠OPC=90°,
则P一定在以OC为圆心,以OC为直径的圆上,圆心坐标是(5,0),半径是5.
则(x-5)2+(kx+4)2=25,
即(k2+1)x2+(8k-10)x+16=0,
△=-160k+36=0,
解得:k=
.
故答案是:
.
点P在直线y=kx+4上移动时,只存在一个点P使∠OPC=90°,
则P一定在以OC为圆心,以OC为直径的圆上,圆心坐标是(5,0),半径是5.
则(x-5)2+(kx+4)2=25,
即(k2+1)x2+(8k-10)x+16=0,
△=-160k+36=0,
解得:k=
| 9 |
| 40 |
故答案是:
| 9 |
| 40 |
点评:本题考查了一次函数与圆以及一元二次方程的综合,理解P一定在以OC为圆心,以OC为直径的圆上,圆心坐标是(5,0),半径是5,是关键.

练习册系列答案
相关题目
下列说法正确的是( )
| A、三角形的内心是这个三角形三条边中垂线的交点 |
| B、矩形的对角线相等的逆命题是真命题 |
| C、一组数据2、9、7、5、4、8、5、3的中位数是5 |
| D、正六边形的外角和是720度 |
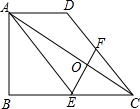 已知:如图,在梯形ABCD中,AD∥BC,∠ABC=90°,BC=2AD,点E是BC的中点、F是CD上的点,联结AE、EF、AC.
已知:如图,在梯形ABCD中,AD∥BC,∠ABC=90°,BC=2AD,点E是BC的中点、F是CD上的点,联结AE、EF、AC.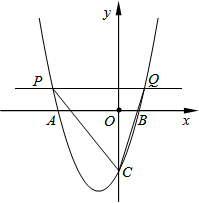 如图,在平面直角坐标系xOy中,二次函数y=ax2+bx-3(a,b是常数)的图象与x轴交于点A(-3,0)和点B(1,0),与y轴交于点C.动直线y=t(t为常数)与抛物线交于不同的两点P、Q.
如图,在平面直角坐标系xOy中,二次函数y=ax2+bx-3(a,b是常数)的图象与x轴交于点A(-3,0)和点B(1,0),与y轴交于点C.动直线y=t(t为常数)与抛物线交于不同的两点P、Q. 某小区现在有一块长方形场地,如图所示,要将这块地划分为四块分别种植兰花、菊花、月季、牵牛花,种植月季的场地长用y表示,宽用x表示.
某小区现在有一块长方形场地,如图所示,要将这块地划分为四块分别种植兰花、菊花、月季、牵牛花,种植月季的场地长用y表示,宽用x表示.