题目内容
17.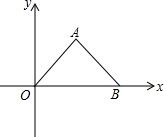 若将等腰直角三角形AOB按如图所示放置,OB=2,则点A关于原点对称的点的坐标为(-1,-1).
若将等腰直角三角形AOB按如图所示放置,OB=2,则点A关于原点对称的点的坐标为(-1,-1).
分析 过点A作AD⊥OB于点D,根据等腰直角三角形的性质求出OD及AD的长,故可得出A点坐标,再由关于原点对称的点的坐标特点即可得出结论.
解答  解:过点A作AD⊥OB于点D,
解:过点A作AD⊥OB于点D,
∵△AOB是等腰直角三角形,OB=2,
∴OD=AD=1,
∴A(1,1),
∴点A关于原点对称的点的坐标为(-1,-1).
故答案为(-1,-1).
点评 本题考查的是关于原点对称的点的坐标特点,熟知等腰直角三角形的性质是解答此题的关键.

练习册系列答案
相关题目
8. 如图,要使?ABCD成为菱形,则需添加的一个条件是( )
如图,要使?ABCD成为菱形,则需添加的一个条件是( )
 如图,要使?ABCD成为菱形,则需添加的一个条件是( )
如图,要使?ABCD成为菱形,则需添加的一个条件是( )| A. | AC=AD | B. | BA=BC | C. | ∠ABC=90° | D. | AC=BD |
9.若(ax2-2xy+y2)-(-ax2+bxy+2y2)=6x2-9xy+cy2成立,则a,b,c的值分别为( )
| A. | 3,-7,-1 | B. | -3,7,-1 | C. | 3,7,-1 | D. | -3,-7,1 |
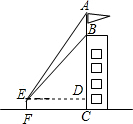 如图,为测量某建筑物BC上旗杆AB的高度,小明在距离建筑物BC底部11.4米的点F处,测得视线与水平线夹角∠AED=60°,∠BED=45°.小明的观测点与地面的距离EF为1.6米.
如图,为测量某建筑物BC上旗杆AB的高度,小明在距离建筑物BC底部11.4米的点F处,测得视线与水平线夹角∠AED=60°,∠BED=45°.小明的观测点与地面的距离EF为1.6米.