题目内容
6.计算:$\frac{2}{{x}^{2}-x-2}$-$\frac{3}{{x}^{2}+5x+4}$.分析 先通分,然后进行同分母分式加减运算,最后要注意将结果化为最简分式.
解答 解:原式=$\frac{2}{(x-2)(x+1)}$-$\frac{3}{(x+1)(x+4)}$,
=$\frac{2(x+4)-3(x-2)}{(x-2)(x+1)(x+4)}$,
=$\frac{14-x}{(x-2)(x+1)(x+4)}$.
点评 本题考查了分式的加减运算,题目比较容易.
异分母分式加减法法则:把分母不相同的几个分式化成分母相同的分式,叫做通分,经过通分,异分母分式的加减就转化为同分母分式的加减.

练习册系列答案
相关题目
16.△ABC的两条高的长度分别为4和12,若第三条高也为整数,则第三条高的长度是( )
| A. | 4 | B. | 4或5 | C. | 5或6 | D. | 6 |
18.当$\frac{|a|}{a}$+$\frac{b}{|b|}$=0时,a与b的关系是( )
| A. | a与b互为相反数 | B. | a=1,b=1 | C. | a与b异号 | D. | a=b=0 |
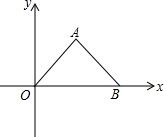 若将等腰直角三角形AOB按如图所示放置,OB=2,则点A关于原点对称的点的坐标为(-1,-1).
若将等腰直角三角形AOB按如图所示放置,OB=2,则点A关于原点对称的点的坐标为(-1,-1). 已知数a与数b所表示的点在数轴上如图所示,则|a+b|-a=b.
已知数a与数b所表示的点在数轴上如图所示,则|a+b|-a=b.