题目内容
7.解方程组:$\left\{\begin{array}{l}{5x+6y-8z=12}\\{x+4y-z=-1}\\{2x+3y-4z=5}\end{array}\right.$.分析 方程组第二个方程变形后,结合其他方程利用加减消元法求出解即可.
解答 解:$\left\{\begin{array}{l}{5x+6y-8z=12①}\\{x+4y-z=-1②}\\{2x+3y-4z=5③}\end{array}\right.$,
②×5-①得:14y+3z=-17④,
②×2-③得:5y+2z=-7⑤,
④×2-⑤×3得:13y=-13,即y=-1,
把y=-1代入⑤得:z=-1,
把y=-1,z=-10代入②得:x=2,
则方程组的解为$\left\{\begin{array}{l}x=2\\ y=-1\\ z=-1\end{array}\right.$.
点评 此题考查了解三元一次方程组,利用了消元的思想,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
18.当$\frac{|a|}{a}$+$\frac{b}{|b|}$=0时,a与b的关系是( )
| A. | a与b互为相反数 | B. | a=1,b=1 | C. | a与b异号 | D. | a=b=0 |
19.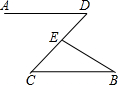 如图,AD∥CB,∠D=43°,∠B=25°,则∠DEB的度数为( )
如图,AD∥CB,∠D=43°,∠B=25°,则∠DEB的度数为( )
 如图,AD∥CB,∠D=43°,∠B=25°,则∠DEB的度数为( )
如图,AD∥CB,∠D=43°,∠B=25°,则∠DEB的度数为( )| A. | 72° | B. | 68° | C. | 63° | D. | 18° |
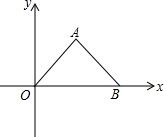 若将等腰直角三角形AOB按如图所示放置,OB=2,则点A关于原点对称的点的坐标为(-1,-1).
若将等腰直角三角形AOB按如图所示放置,OB=2,则点A关于原点对称的点的坐标为(-1,-1).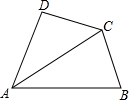 在四边形ABCD中,∠ABC+∠ADC=180°,CB=CD.求证:AC平分∠BAD.
在四边形ABCD中,∠ABC+∠ADC=180°,CB=CD.求证:AC平分∠BAD.