题目内容
16.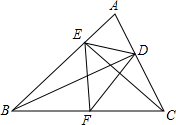 如图,在锐角△ABC中,BD、CE为高,F为BC的中点,连接DE、DF、EF,则结论:①DE=EF;②AD:AB=AE:AC;③△AEC∽△ADB;④AE+AD=BC,其中正确结论的序号是②③(写上所有正确结论的序号)
如图,在锐角△ABC中,BD、CE为高,F为BC的中点,连接DE、DF、EF,则结论:①DE=EF;②AD:AB=AE:AC;③△AEC∽△ADB;④AE+AD=BC,其中正确结论的序号是②③(写上所有正确结论的序号)
分析 由已知条件和直角三角形斜边上的中线性质得出EF=$\frac{1}{2}$BC,DF=$\frac{1}{2}$BC,得出EF=DF,①不正确;
证明B、C、D、E四点共圆,由圆周角定理得出∠ADE=∠ABC,∠ABD=∠ACE,证出△ADE∽△ABC,得出AD:AB=AE:AC,②正确;
由相似三角形的判定方法得出△AEC∽△ADB,③正确;不能得出AE+AD=BC,即可得出结果.
解答 解:∵BD、CE为高,
∴∠BEC=∠AEC=∠BDC=∠BDA=90°,
∵F为BC的中点,
∴EF=$\frac{1}{2}$BC,DF=$\frac{1}{2}$BC,
∴EF=DF,①不正确;
∵∠BEC=∠BDC=90°,
∴B、C、D、E四点共圆,
∴∠ADE=∠ABC,∠ABD=∠ACE,
又∵∠A=∠A,
∴△ADE∽△ABC,
∴AD:AB=AE:AC,②正确;
∵∠A=∠A,
∴△AEC∽△ADB,③正确;
不能得出AE+AD=BC,④不正确;
故答案为:②③.
点评 本题考查了相似三角形的判定与性质、四点共圆、圆周角定理等知识;熟练掌握四点共圆,由圆周角定理得出三角形相似是解决问题的关键.

练习册系列答案
相关题目
1.下列各组条件中,能判断两个直角三角形全等的是( )
| A. | 一组边对应相等 | B. | 两组直角边对应相等 | ||
| C. | 两组锐角对应相等 | D. | 一组锐角对应相等 |
6.下列函数是一次函数的是( )
| A. | y=kx+2 | B. | y=-$\frac{6}{x}$ | C. | y=-3x2+2 | D. | y=-$\frac{x}{4}$ |
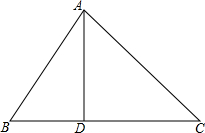 如图,D是△ABC中BC边上一点,∠B=∠DAC,AB2=BD•BC.求证:△ABD∽△CAD.
如图,D是△ABC中BC边上一点,∠B=∠DAC,AB2=BD•BC.求证:△ABD∽△CAD.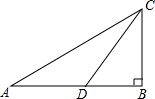 如图,Rt△ABC中,∠ABC=90°,点D在直角边AB上,且∠DCB=∠A.
如图,Rt△ABC中,∠ABC=90°,点D在直角边AB上,且∠DCB=∠A.