题目内容
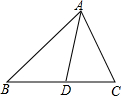
7.若一个三角形的三边长分别为$\sqrt{10}$,$\sqrt{5}$,2,与这个三角形相似的三角形有两边长分别为$\sqrt{2}$,$\frac{2}{5}$$\sqrt{5}$,则第三边长为1.分析 根据相似三角形的性质得出相似比进而求出答案.
解答 解:∵一个三角形的三边长分别为$\sqrt{10}$,$\sqrt{5}$,2,与这个三角形相似的三角形有两边长分别为$\sqrt{2}$,$\frac{2}{5}$$\sqrt{5}$,
且$\frac{\sqrt{10}}{\sqrt{2}}$=$\sqrt{5}$,$\frac{2}{\frac{2}{5}\sqrt{5}}$=$\sqrt{5}$,
∴设第三边长为x,
故$\frac{\sqrt{5}}{x}$=$\sqrt{5}$,
解得:x=1,
故第三边长为:1.
故答案为:1.
点评 此题主要考查了相似三角形的性质,正确得出对应边是解题关键.

练习册系列答案
 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
2.在下列整式中,次数为3的单项式是( )
| A. | ab2 | B. | x3-y3 | C. | m3n | D. | 3st |
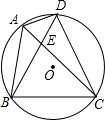 如图,四边形ABCD内接于⊙O,连接AC和BD相交于E,且AC平分∠BAD,求证:BC2=AC•CE.
如图,四边形ABCD内接于⊙O,连接AC和BD相交于E,且AC平分∠BAD,求证:BC2=AC•CE.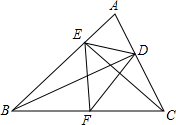 如图,在锐角△ABC中,BD、CE为高,F为BC的中点,连接DE、DF、EF,则结论:①DE=EF;②AD:AB=AE:AC;③△AEC∽△ADB;④AE+AD=BC,其中正确结论的序号是②③(写上所有正确结论的序号)
如图,在锐角△ABC中,BD、CE为高,F为BC的中点,连接DE、DF、EF,则结论:①DE=EF;②AD:AB=AE:AC;③△AEC∽△ADB;④AE+AD=BC,其中正确结论的序号是②③(写上所有正确结论的序号)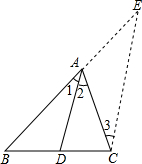 请阅读下面的材料,并回答所提出的问题.
请阅读下面的材料,并回答所提出的问题.