题目内容
4.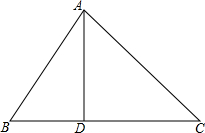 如图,D是△ABC中BC边上一点,∠B=∠DAC,AB2=BD•BC.求证:△ABD∽△CAD.
如图,D是△ABC中BC边上一点,∠B=∠DAC,AB2=BD•BC.求证:△ABD∽△CAD.
分析 根据AB2=BD•BC及∠B=∠B证得△ABD∽△CBA,由相似三角形性质可得∠BAD=∠C,结合∠B=∠DAC得证.
解答 证明:∵AB2=BD•BC,
∴$\frac{AB}{BC}=\frac{BD}{AB}$,
∵∠ABD=∠CBA,
∴△ABD∽△CBA,
∴∠BAD=∠C,
又∵∠B=∠DAC,
∴△ABD∽△CAD.
点评 本题主要考查相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
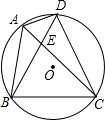 如图,四边形ABCD内接于⊙O,连接AC和BD相交于E,且AC平分∠BAD,求证:BC2=AC•CE.
如图,四边形ABCD内接于⊙O,连接AC和BD相交于E,且AC平分∠BAD,求证:BC2=AC•CE. △ABD中,AB=AD,∠BAD=90°,P为直线AB上一动点,AE⊥DP于E,交直线BD于F.
△ABD中,AB=AD,∠BAD=90°,P为直线AB上一动点,AE⊥DP于E,交直线BD于F.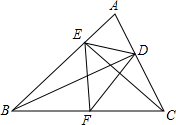 如图,在锐角△ABC中,BD、CE为高,F为BC的中点,连接DE、DF、EF,则结论:①DE=EF;②AD:AB=AE:AC;③△AEC∽△ADB;④AE+AD=BC,其中正确结论的序号是②③(写上所有正确结论的序号)
如图,在锐角△ABC中,BD、CE为高,F为BC的中点,连接DE、DF、EF,则结论:①DE=EF;②AD:AB=AE:AC;③△AEC∽△ADB;④AE+AD=BC,其中正确结论的序号是②③(写上所有正确结论的序号)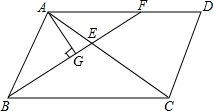 如图,在平行四边形ABCD中,AB=3,BC=5,点F是AD上的一点,且DF=2,连接BF交AC于点E.
如图,在平行四边形ABCD中,AB=3,BC=5,点F是AD上的一点,且DF=2,连接BF交AC于点E.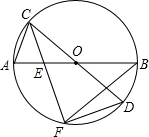 如图,AB、CD为⊙O的直径,E为OA的中点,直线CE交⊙O于另一点F,连接DF,若⊙O的半径为4,DF=$\sqrt{15}$,CE<EF
如图,AB、CD为⊙O的直径,E为OA的中点,直线CE交⊙O于另一点F,连接DF,若⊙O的半径为4,DF=$\sqrt{15}$,CE<EF