题目内容
2.若关于x的方程x2-2ax+a+2=0有两个不相等的实根,求分别满足下列条件的a的取值范围:(1)两根都大于1;
(2)一根大于1,一根小于1;
(3)两根都小于1.
分析 由关于x的方程x2-2ax+a+2=0有两个不相等的实根,得出△=(-2a)2-4(a+2)>0,解得a<-1或a>2.设方程x2-2ax+a+2=0的两根为α,β,利用根与系数的关系得到α+β=2a,αβ=a+2.
(1)由两根都大于1,得出(α-1)(β-1)>0,且对称轴-$\frac{-2a}{2}$>1,依此求出a的取值范围;
(2)由一根大于1,一根小于1,得出(α-1)(β-1)<0,依此求出a的取值范围;
(3)由两根都小于1,得出(α-1)(β-1)>0,且对称轴-$\frac{-2a}{2}$<1,依此求出a的取值范围.
解答 解:∵关于x的方程x2-2ax+a+2=0有两个不相等的实根,
∴△=(-2a)2-4(a+2)>0,
∴a<-1或a>2.
设方程x2-2ax+a+2=0的两根为α,β,
α+β=2a,αβ=a+2.
(1)∵两根都大于1,
∴(α-1)(β-1)>0,
∴αβ-(α+β)+1>0,
∴a+2-2a>-1,
∴a<3,
又-$\frac{-2a}{2}$>1,a>1;
又a<-1或a>2,
∴2<a<3;
(2)∵一根大于1,一根小于1,
∴(α-1)(β-1)<0,
∴αβ-(α+β)+1<0,
∴a+2-2a<-1,
∴a>3,
∴a>3;
(3)∵两根都小于1,
∴(α-1)(β-1)>0,
∴αβ-(α+β)+1>0,
∴a+2-2a>-1,
∴a<3,
又-$\frac{-2a}{2}$<1,a<1;
又a<-1或a>2,
∴a<-1.
点评 本题考查了根的判别式,根与系数的关系,属于基础题,关键是要熟记x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
相关题目
17. 随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A,B两种上网学习的月收费方式:
随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A,B两种上网学习的月收费方式:
设每月上网学习时间为x小时,方案A,B的收费金额分别为yA,yB.
(1)如图是yB与x之间函数关系的图象,请根据图象填空:m=10;n=50
(2)写出yA与x之间的函数关系式.
(3)选择哪种方式上网学习合算,为什么?
 随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A,B两种上网学习的月收费方式:
随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A,B两种上网学习的月收费方式:| 收费方式 | 月使用费/元 | 包时上网时间/h | 超时费/(元/min) |
| A | 7 | 25 | 0.01 |
| B | m | n | 0.01 |
(1)如图是yB与x之间函数关系的图象,请根据图象填空:m=10;n=50
(2)写出yA与x之间的函数关系式.
(3)选择哪种方式上网学习合算,为什么?
10. 如图,AO⊥BO,CO⊥DO,∠AOC:∠BOC=1:5,则∠BOD=( )
如图,AO⊥BO,CO⊥DO,∠AOC:∠BOC=1:5,则∠BOD=( )
 如图,AO⊥BO,CO⊥DO,∠AOC:∠BOC=1:5,则∠BOD=( )
如图,AO⊥BO,CO⊥DO,∠AOC:∠BOC=1:5,则∠BOD=( )| A. | 105° | B. | 112.5° | C. | 135° | D. | 157.5° |
 在矩形ABCD中,AB=a,AD=b,点M为BC边上一动点(点M与点B、C不重合),连接AM,过点M作MN⊥AM,垂足为M,MN交CD或CD的延长线于点N.
在矩形ABCD中,AB=a,AD=b,点M为BC边上一动点(点M与点B、C不重合),连接AM,过点M作MN⊥AM,垂足为M,MN交CD或CD的延长线于点N.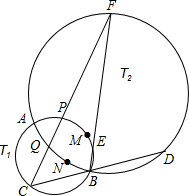 如图,两圆T1、T2相交于A、B两点,过点B的一条直线分别交圆T1、T2于点C、D,过点B的另一条直线分别交圆T1、T2于点E、F,直线CF分别交圆T1、T2于点P、Q,设M、N分别是弧PB、弧QB的中点,求证:若CD=EF,则C、F、M、N四点共圆.
如图,两圆T1、T2相交于A、B两点,过点B的一条直线分别交圆T1、T2于点C、D,过点B的另一条直线分别交圆T1、T2于点E、F,直线CF分别交圆T1、T2于点P、Q,设M、N分别是弧PB、弧QB的中点,求证:若CD=EF,则C、F、M、N四点共圆.