计算:($\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+-+$\frac{1}{2008}$)(1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+-+$\frac{1}{2007}$)-(1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+-+$\frac{1}{2008}$)($\frac 题目和参考答案——青夏教育精英家教网—

题目内容

14．计算：（$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+…+$\frac{1}{2008}$）（1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+…+$\frac{1}{2007}$）-（1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+…+$\frac{1}{2008}$）（$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+…+$\frac{1}{2007}$）

分析设x=$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+…+$\frac{1}{2007}$，代入所求的式子，然后进行化简即可求解．

解答解：设x=$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+…+$\frac{1}{2007}$，则原式=（x+$\frac{1}{2008}$）（1+x）-（1+x+$\frac{1}{2008}$）x
=x+$\frac{1}{2008}$+x²+$\frac{1}{2008}$x-（x+x²+$\frac{1}{2008}$x）
=x+$\frac{1}{2008}$+x²+$\frac{1}{2008}$x-x-x²-$\frac{1}{2008}$x
=$\frac{1}{2008}$．

点评本题考查了整式的混合运算，正确设出未知数是关键．

练习册系列答案

5．某中学初二年级抽取部分学生进行跳绳测试．并规定：每分钟跳90次以下的为不及格；每分钟跳90～99次的为及格；每分钟跳100～109次的为中等；每分钟跳110～119次的为良好；每分钟跳120次及以上的为优秀．测试结果整理绘制成如下两幅不完整的统计图．请根据图中信息，解答下列各题：
（1）参加这次跳绳测试的共有50人；
（2）补全条形统计图；
（3）在扇形统计图中，“中等”部分所对应的圆心角的度数是72°；
（4）如果该校初二年级的总人数是480人，根据此统计数据，请你估算该校初二年级跳绳成绩为“优秀”的人数．

2．若关于x的方程x²-2ax+a+2=0有两个不相等的实根，求分别满足下列条件的a的取值范围：
（1）两根都大于1；
（2）一根大于1，一根小于1；
（3）两根都小于1．

9．

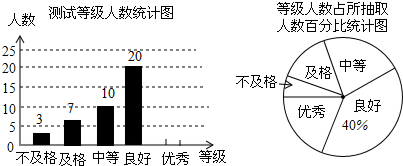
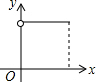
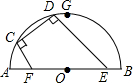如图，AB为半圆所在⊙O的直径，弦CD为定长且小于⊙O的半径（C点与A点不重合），CF⊥CD交AB于点F，DE⊥CD交AB于点E，G为半圆弧上的中点．当点C在$\widehat{AG}$上运动时，设$\widehat{AG}$的长为x，CF+DE=y．则下列图象中，能表示y与x的函数关系的图象大致是（　　）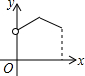

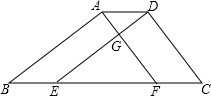19．

如图，四边形ABED与四边形AFCD都是平行四边形，AF和DE相交成直角，AG=3cm，DG=4cm，?ABCD的面积为36cm²，求四边形ABCD的周长．

4．若关于x的方程x²-2（1-k）x+k²=0有实数根m和n，则m+n的取值范围是（　　）

	A．	同位角相等
	B．	两边和一角对应相等的两个三角形全等
	C．	面积相等的两个三角形全等
	D．	等腰三角形底边中点到两腰的距离相等

2．

如图，已知在正方形ABCD中，AE=EB，AF=$\frac{1}{4}$AD，求证：CE⊥EF．

试题分类