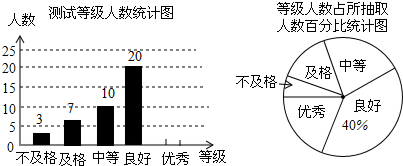
题目内容
13. 在矩形ABCD中,AB=a,AD=b,点M为BC边上一动点(点M与点B、C不重合),连接AM,过点M作MN⊥AM,垂足为M,MN交CD或CD的延长线于点N.
在矩形ABCD中,AB=a,AD=b,点M为BC边上一动点(点M与点B、C不重合),连接AM,过点M作MN⊥AM,垂足为M,MN交CD或CD的延长线于点N.(1)求证:△CMN∽△BAM;
(2)设BM=x,CN=y,求y关于x的函数解析式.当x取何值时,y有最大值,并求出y的最大值;
(3)当点M在BC上运动时,求使得下列两个条件都成立的b的取值范围:①点N始终在线段CD上,②点M在某一位置时,点N恰好与点D重合.
分析 (1)由四边形ABCD是矩形可得∠B=∠C=90°,要证△CMN∽△BAM,只需证∠BAM=∠CMN即可;
(2)根据相似三角形的性质,由△CMN∽△BAM即可得到y与x的函数解析式,然后只需运用配方法就可求出y的最大值;
(3)由点M在BC上运动(点M与点B、C不重合),可得0<x<b,要满足条件①,应保证当0<x<b时,y≤a恒成立,要满足条件②,需存在一个x,使得y=a,综合条件①和②,当0<x<b时y最大值应为a,然后结合(2)中的结论,就可解决问题.
解答 解:(1)∵四边形ABCD是矩形,
∴∠B=∠C=90°,
∴∠BAM+∠AMB=90°.
∵MN⊥AM,即∠AMN=90°,
∴∠CMN+∠AMB=90°,
∴∠BAM=∠CMN,
∴△CMN∽△BAM;
(2)∵△CMN∽△BAM,
∴$\frac{CM}{BA}$=$\frac{CN}{BM}$.
∵BM=x,CN=y,AB=a,BC=AD=b,
∴$\frac{b-x}{a}$=$\frac{y}{x}$,
∴y=$\frac{1}{a}$(bx-x2)=-$\frac{1}{a}$(x2-bx)
=-$\frac{1}{a}$[(x-$\frac{b}{2}$)2-$\frac{{b}^{2}}{4}$]
=-$\frac{1}{a}$(x-$\frac{b}{2}$)2+$\frac{{b}^{2}}{4a}$.
∵-$\frac{1}{a}$<0,
∴当x=$\frac{b}{2}$时,y取最大值,最大值为$\frac{{b}^{2}}{4a}$.
(3)由题可知:
当0<x<b时,y的最大值为a,即$\frac{{b}^{2}}{4a}$=a,
解得:b=2a.
∴要同时满足两个条件,b的值为2a.
点评 本题主要考查了相似三角形的判定与性质、矩形的性质、二次函数的最值性,运用配方法是解决第(2)小题的关键.需要说明的是,对于第(3)小题,要满足条件①,只需$\frac{{b}^{2}}{4a}$≤a即可,但$\frac{{b}^{2}}{4a}$<a时,不满足条件②,故要同时满足条件①和②,只有$\frac{{b}^{2}}{4a}$=a时才成立.

| A. | 同位角相等 | |
| B. | 两边和一角对应相等的两个三角形全等 | |
| C. | 面积相等的两个三角形全等 | |
| D. | 等腰三角形底边中点到两腰的距离相等 |
 一块四边形绿化园地,四角向外都做有半径为6的扇形喷水池(阴影部分),则这四个喷水池面积和为106π(结果保留π).
一块四边形绿化园地,四角向外都做有半径为6的扇形喷水池(阴影部分),则这四个喷水池面积和为106π(结果保留π).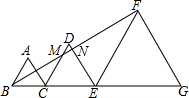 如图,△ABC、△DCE、△FEG为等边三角形,边长分别为2、3、5,且从左至右如图排列,连接BF,交DC、DE分别于M、N两点,则△DMN的面积为$\frac{\sqrt{3}}{8}$.
如图,△ABC、△DCE、△FEG为等边三角形,边长分别为2、3、5,且从左至右如图排列,连接BF,交DC、DE分别于M、N两点,则△DMN的面积为$\frac{\sqrt{3}}{8}$.
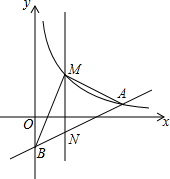 如图,在平面直角坐标系中,已知点A(8,1),B(0,-3),反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A,动直线x=t(0<t<8)与反比例函数的图象交于点M,与直线AB交于点N.
如图,在平面直角坐标系中,已知点A(8,1),B(0,-3),反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A,动直线x=t(0<t<8)与反比例函数的图象交于点M,与直线AB交于点N.