Question

5．我们已经知道函数y=$\frac{1}{x}$与y=-$\frac{1}{x}$的两个图象之间的联系与区别，那你知道函数y=$\frac{1}{|x|}$的图象与上述两个函数图象之间又有怎样的关系吗？
（1）试用描点法画出图象加以探究；
（2）如果利用y=$\frac{1}{|x|}$与y=$\frac{1}{x}$或y=-$\frac{1}{x}$的图象之间的关系，可怎样画y=-$\frac{2}{|x|}$的图象？

Answer 1

分析 （1）首先用描点法画出y=$\frac{1}{|x|}$的图象；然后探究出y=$\frac{1}{|x|}$的图象与函数y=$\frac{1}{x}$与y=-$\frac{1}{x}$的两个图象之间的关系即可．
（2）首先把y=$\frac{1}{x}$或y=-$\frac{1}{x}$的图象的横坐标不变，纵坐标扩大到原来的2倍；然后取函数y=$\frac{2}{x}$与y=-$\frac{2}{x}$的两个图象在y轴下方的部分，即可画出y=-$\frac{2}{|x|}$的图象．

解答 解：（1）如图1，，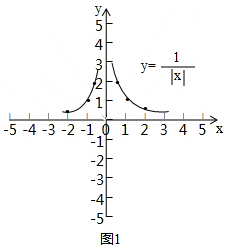
y=$\frac{1}{|x|}$的图象与函数y=$\frac{1}{x}$与y=-$\frac{1}{x}$的两个图象之间的关系为：
取函数y=$\frac{1}{x}$与y=-$\frac{1}{x}$的两个图象在y轴上方的部分．

（2）如图2，，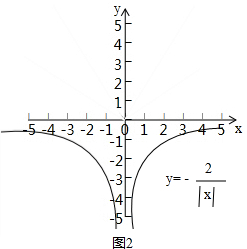
取函数y=$\frac{2}{x}$与y=-$\frac{2}{x}$的两个图象在y轴下方的部分，即为y=-$\frac{2}{|x|}$的图象．

点评 此题主要考查了反比例函数的性质，以及根据反比例函数的性质作图的能力，要熟练掌握，解答此题的关键是要明确：（1）反比例函数y=xk（k≠0）的图象是双曲线；（2）当k＞0，双曲线的两支分别位于第一、第三象限，在每一象限内y随x的增大而减小；（3）当k＜0，双曲线的两支分别位于第二、第四象限，在每一象限内y随x的增大而增大．