题目内容
15..已知三角形的三边长分别是a、b、c,且a>c,那么|c-a|-$\sqrt{(a+c-b)^{2}}$=b-2c.分析 根据题意判断c-a的符号,根据三角形的三边关系,判断a+c-b的符号,根据二次根式的性质化简、合并同类项即可得到答案.
解答 解:∵a>c,∴c-a<0,
∵a、b、c分别是三角形的三边长,∴a+c-b>0,
∴|c-a|-$\sqrt{(a+c-b)^{2}}$=a-c-a-c+b=b-2c,
故答案为:b-2c.
点评 本题考查的是三角形的三边关系和二次根式的性质,掌握任意两边之和大于第三边,任意两边之差小于第三边和二次根式的性质是解题的关键.

练习册系列答案
相关题目
13.一组数:8,9,7,10,6,9,9,6,则这组数的中位数与众数的和是( )
| A. | 16.5 | B. | 17 | C. | 17.5 | D. | 18 |
3.下列各数中:0、-$\sqrt{2}$、$\root{3}{8}$、$\frac{5}{13}$、π、0.3737737773…(它的位数无限且相邻两个“3”之间“7”的个数依次加1个),无理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.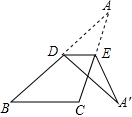 如图,在△ABC中,D,E分别是边AB,AC的中点,∠B=30°.现将△ADE沿DE折叠,点A落在三角形所在平面内的点为A′,则∠BDA′的度数为( )
如图,在△ABC中,D,E分别是边AB,AC的中点,∠B=30°.现将△ADE沿DE折叠,点A落在三角形所在平面内的点为A′,则∠BDA′的度数为( )
 如图,在△ABC中,D,E分别是边AB,AC的中点,∠B=30°.现将△ADE沿DE折叠,点A落在三角形所在平面内的点为A′,则∠BDA′的度数为( )
如图,在△ABC中,D,E分别是边AB,AC的中点,∠B=30°.现将△ADE沿DE折叠,点A落在三角形所在平面内的点为A′,则∠BDA′的度数为( )| A. | 100° | B. | 120° | C. | 130° | D. | 140° |
4.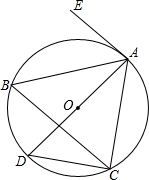 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,EA是⊙O的切线.若∠EAC=120°,则∠ABC的度数是( )
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,EA是⊙O的切线.若∠EAC=120°,则∠ABC的度数是( )
 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,EA是⊙O的切线.若∠EAC=120°,则∠ABC的度数是( )
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,EA是⊙O的切线.若∠EAC=120°,则∠ABC的度数是( )| A. | 80° | B. | 70° | C. | 60° | D. | 50° |